Easy is Perfect

[백준] 2263번 C/C++ 풀이 _ 트리의 순회

  • melonicedlatte
  • Feb 04, 2018


> 출처 : https://www.acmicpc.net/problem/2263 

> 문제 설명 : 

트리의 순회

시간 제한메모리 제한제출정답맞은 사람정답 비율
5 초128 MB140257241141.684%

문제

n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 n(1≤n≤100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.

출력

첫째 줄에 프리오더를 출력한다.

예제 입력 

3
1 2 3
1 3 2

예제 출력 

2 1 3

> 풀이 방법 

문제를 보고 딱 어떻게 풀어야 할 지 감이 잘 오지 않았다. 
파트가 분할 정복이라 분할 정복의 방식으로 생각해보았다. 

풀이 방법을 생각하고도 어마어마한 시간이 걸려서 문제를 해결했는데, 차차 시간을 줄여가야겠다. 
그리고 더 엄밀하게 설계를 한 다음에 코딩에 들어가야 되겠다.
( 코딩을 하면서 문제를 발견하는 것도 있어서 과연 그게 정답인지는 잘 모르겠지만.  )

문제 풀이 방식은 아래와  같다. 

먼저 아래와 같은 트리를 생각해보고, 실제 순서를 프리오더, 인오더, 포스트오더에 따라서 기입해보았다. 


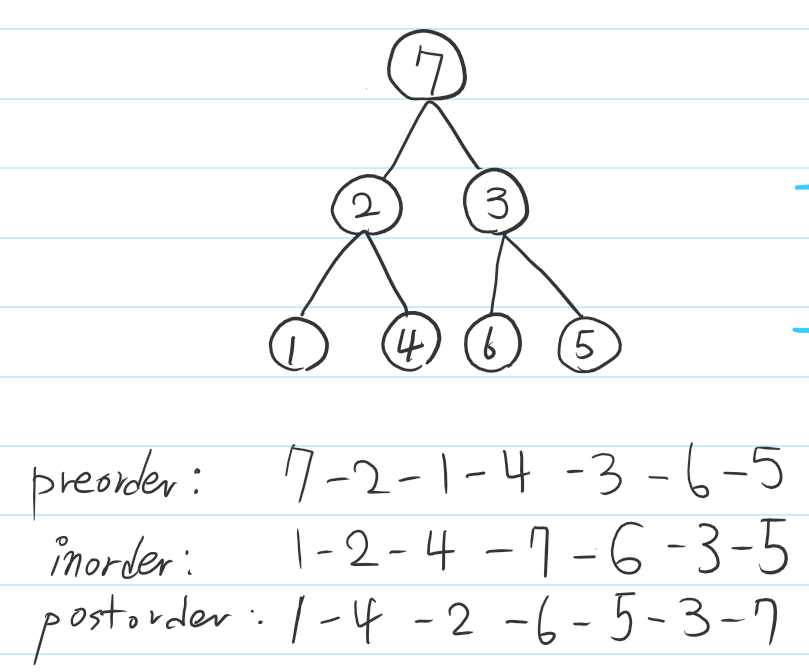
여기에서 특징을 살펴보면 가장 최상단의 '루트노드' 가 postorder 에서는 가장 마지막에 나타나고, 
inorder는 '루트노드' 가 나타나는 곳에서 왼쪽은 '루트노드의 왼쪽 자식 노드' 가 되고, 오른쪽은 '루트노드의 오른쪽 자식노드' 가 된다. 

아래와 같이 표현해보자. 
루트노드의 자식노드는 인오더와 포스트오더에서 동일하기 때문에, l 과 r 의 사이즈는 동일하다.


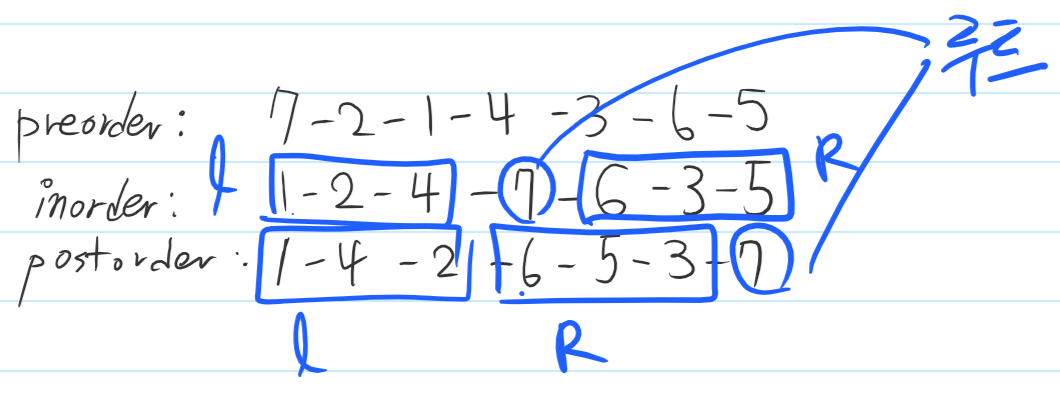
이를 일반화하면 아래와 같다. 
맨 처음에 주어진 인오더와 포스트오더를 루트노드를 찾아 루트노드의 좌우 노드를 찾아본다. 
그 다음에는 루트노드의 자식노드의 각각을 다시 하나의 트리로 여기고,
자식노드의 inorder, postorder의 시작과 끝 index 를 인자로 넘겨서 또 분할해준다. 

이와 같은 식으로 해주면, 이전 단계에서 찾은 루트노드의 왼쪽자식에 왼쪽 자식의 트리에서 만든 루트노드를 다시 연결해주고,
오른쪽 자식의 트리에서 루트노드를 이전 단계에서 찾은 루트노드의 오른쪽 자식으로 넣어준다.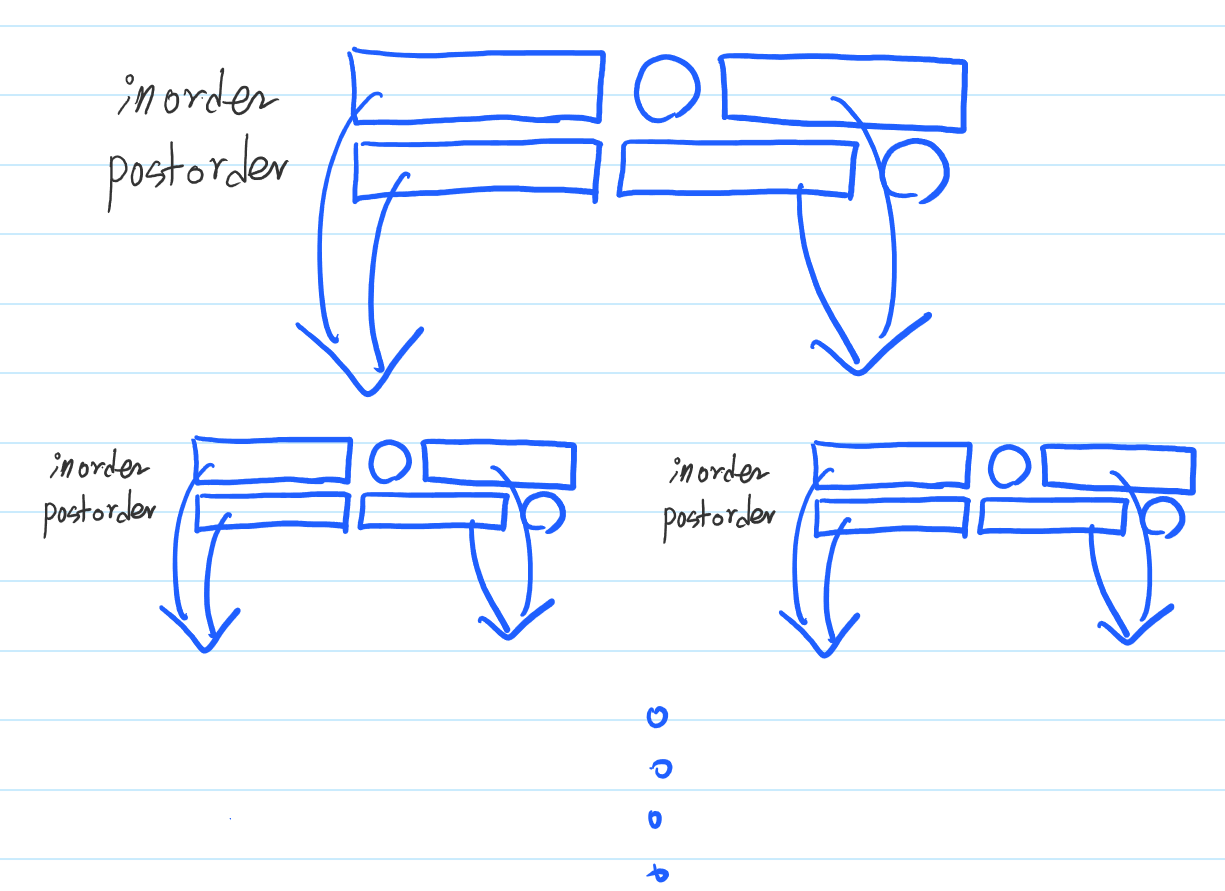 

이와 같은 식으로 계속해서 진행해준다. 
진행하다가 inorder와 postorder 의 시작, 끝 인덱스에서 시작이 끝보다 크면 바로 리턴하고, 
동일할 경우에는 해당 노드가 단말노드이기 때문에 이전 단계의 부모의 자식으로 넣어주고 리턴한다. 

소스코드는 아래와 같다. 
설명이 좀 미약한데 앞으로는 주석을 더 열심히 달아야겠다. 

> 풀이 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <iostream> 
#include <vector> 
 
using namespace std;
 
typedef struct tree_node {
    int value = -1;
    tree_node* left;
    tree_node* right;
}tree_node;
 
vector<int> inorder_vec;
vector<int> postorder_vec;
tree_node* oldest_parent;
 
void make_tree(int inorder_start, int inorder_end, int postorder_start, int postorder_end, int direction, tree_node* parent) {
    int inorder_parent_index;
 
    if (inorder_start > inorder_end) return;
    if (postorder_start > postorder_end) return;
 
    tree_node* sub_parent = (tree_node*)malloc(sizeof(tree_node));
    sub_parent->left = NULL;
    sub_parent->right = NULL;
    sub_parent->value = postorder_vec.at(postorder_end);
 
    // param == root
    if (direction == 1) {
        oldest_parent = sub_parent;
    }
    // param == left 
    else if (direction == 2) {
        parent->left = sub_parent;
    }
    // param == right 
    else if (direction == 3) {
        parent->right = sub_parent;
    }
 
    if (inorder_start >= inorder_end) return;
 
    for (int i = inorder_start; i <= inorder_end; i++) {
        if (sub_parent->value == inorder_vec[i]) {
            inorder_parent_index = i;
            break;
        }
    }
 
    // right 
    make_tree(inorder_parent_index + 1, inorder_end, postorder_end - (inorder_end - inorder_parent_index), postorder_end - 1, 3, sub_parent);
    // left
    make_tree(inorder_start, inorder_parent_index - 1, postorder_start, postorder_start + (inorder_parent_index - inorder_start) - 1, 2, sub_parent);
}
 
void make_preorder(tree_node* each_node) {
    if (each_node == NULL) return;
    cout << each_node->value << " ";
    make_preorder(each_node->left);
    make_preorder(each_node->right);
}
 
int main() {
    int total_num = 0;
    cin >> total_num;
 
    // making inorder and postorder 
    for (int i = 0; i < total_num; i++) {
        int sub;
        cin >> sub;
        inorder_vec.push_back(sub);
    }
 
    for (int i = 0; i < total_num; i++) {
        int sub;
        cin >> sub;
        postorder_vec.push_back(sub);
    }
 
    // find preorder 
    make_tree(0, total_num - 1, 0, total_num - 1, 1, NULL);
    make_preorder(oldest_parent);
 
    return 0;
}
 
cs



Search