| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 5 초 | 128 MB | 5881 | 1230 | 764 | 22.126% |
문제
해커 김지민은 잘 알려진 어느 회사를 해킹하려고 한다. 이 회사는 N개의 컴퓨터로 이루어져 있다. 김지민은 귀찮기 때문에, 한 번의 해킹으로 여러 개의 컴퓨터를 해킹 할 수 있는 컴퓨터를 해킹하려고 한다.
이 회사의 컴퓨터는 신뢰하는 관계와, 신뢰하지 않는 관계로 이루어져 있는데, A가 B를 신뢰하는 경우에는 B를 해킹하면, A도 해킹할 수 있다는 소리다.
이 회사의 컴퓨터의 신뢰하는 관계가 주어졌을 때, 한 번에 가장 많은 컴퓨터를 해킹할 수 있는 컴퓨터의 번호를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에, N과 M이 들어온다. N은 10,000보다 작거나 같은 자연수, M은 100,000보다 작거나 같은 자연수이다. 둘째 줄부터 M개의 줄에 신뢰하는 관계가 A B와 같은 형식으로 들어오며, "A가 B를 신뢰한다"를 의미한다.
출력
첫째 줄에, 김지민이 한 번에 가장 많은 컴퓨터를 해킹할 수 있는 컴퓨터의 번호를 오름차순으로 출력한다.
예제 입력
5 4 3 1 3 2 4 3 5 3
예제 출력
1 2
힌트
>> 문제 해결 방법
아래와 같이 노드 4 개와 각각의 연결 관계가 이루어져 있다고 가정해보자.
화살표는 1이 2를 신뢰하는 경우에 1 ->2 와 같은 방향으로 나타내었다.
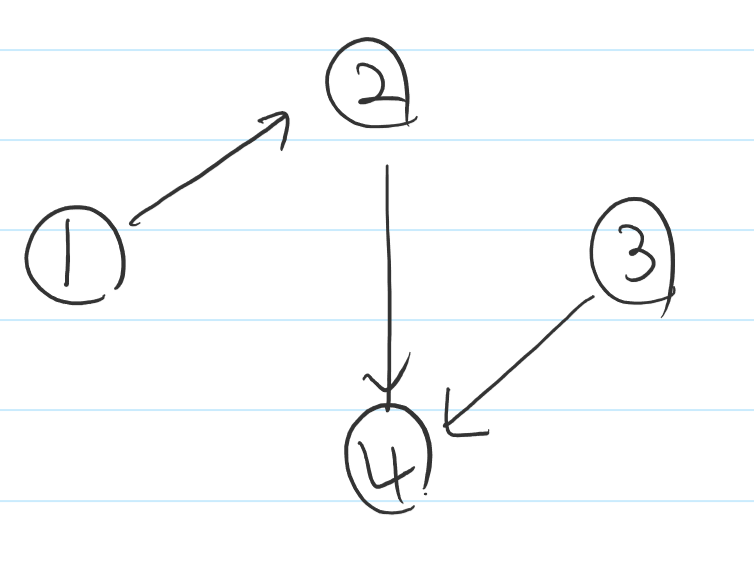
4에 도달하는 화살표는 2개이지만 1번이 2번을 신뢰하여 결국 4번을 신뢰하는 녀석들은 3개이다.
결국 이 문제에서는 "각 노드에서 가지고 있는 모든 자식의 갯수" 가 많은 녀석들을 나열하는 것이 중요하다.
하지만 놓치기 쉬운 문제가 있다. 바로 cycle이다.
위와 같이 해서 먼저 문제 답을 제출했으나, cycle을 고려하지 않을 경우에는 "메모리초과 (out of memory)" 에러가 뜨게 된다.
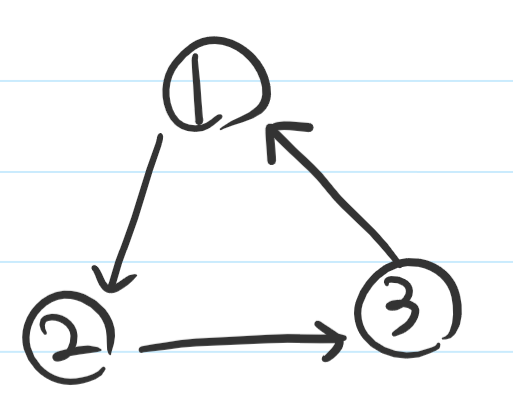
위와 같은 싸이클에서 각각 노드는 자식이 2개라고 볼 수 있고, 모두 정답으로 출력해야 한다.
따라서, 자식 수를 계산 할 때 싸이클이 형성 된 것으로 판단되면 그 시점에서 자식을 추가 되는 것을 중지해야한다.
구현 방법은 아래와 같다.
아래와 같이 구조체 노드를 생성한다.
노드는 트리 구조에서 각 노드를 나타낸다.
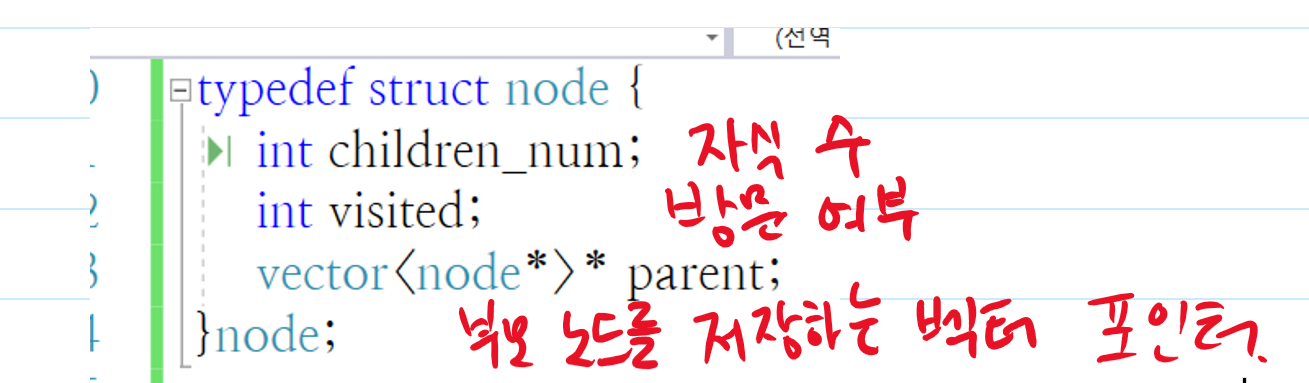
먼저, 프로그램 시작 시에는 위와 같이 정의된 노드 포인터 tree 배열을 생성한다.
그리고 for 문을 돌면서 각각 노드 포인터에 노드들을 할당해주고, 값을 초기화해준다.
그 다음에는 관계들을 연결해줘서 트리를 생성한다.

그리고 아래와 같이 자식 수 체크를 진행해준다.

>> 소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 | #include <iostream> #include <vector> #include <algorithm> #include <queue> using namespace std; // 벡터를 구조체 안에 선언한 다음에 계속해서 push_back 함수를 사용하면 // 구조체의 크기가 동적으로 커지기 때문에 연산이 되지 않는 것 같다. // 따라서 벡터 포인터를 멤버로 설정해준다. typedef struct node { int children_num; int visited; vector<node*>* parent; }node; int total_num; node** tree; vector<int> answers; vector<pair<int, int >> network_vector; queue<node*> find_queue; int main() { int network_num; cin >> total_num >> network_num; tree = (node**)malloc(sizeof(node*)*total_num); // 노드 생성 for (int i = 0; i < total_num; i++) { tree[i] = (node*)malloc(sizeof(node)); tree[i]->parent = new vector<node*>(); tree[i]->visited = 0; tree[i]->children_num = 0; } // 관계 연결 for (int i = 0; i < network_num; i++) { int A, B; cin >> A >> B; network_vector.push_back(pair<int,int>(A, B)); (*(tree[A - 1]->parent)).push_back(tree[B - 1]); } // 자식 수 체크 for (int i = 0; i < total_num ; i++) { node* sub = tree[i]; tree[i]->visited = 1 ; // 네트워크에서 부모들을 전부 children_num 을 추가해줘야 한다. // 부모를 큐에 추가 for (int k = 0; k < (*(sub->parent)).size(); k++) { find_queue.push((*(sub->parent))[k]); } // 상위 부모 탐색 while (find_queue.size()) { sub = find_queue.front(); find_queue.pop(); if (sub->visited == 1) continue; sub->visited = 1; sub->children_num++; for (int k = 0; k < (*(sub->parent)).size(); k++) { find_queue.push((*(sub->parent))[k]); } } for (int j = 0; j < total_num; j++) tree[j]->visited = 0; } // 가장 첫 번째 노드를 일단 최대라고 가정하고 int max = tree[0]->children_num; int max_index = 0; answers.push_back(0); // 최대를 찾는다. 더 큰 놈이 나오면 벡터에 추가해준다. for (int i = 1; i < total_num; i++) { // 최대 찾기 if (max == tree[i]->children_num) { answers.push_back(i); }else if (max < tree[i]->children_num) { answers.clear(); answers = vector<int>(); max = tree[i]->children_num; max_index = i; answers.push_back(i); } } // 정답을 정렬해서 출력해준다. sort(answers.begin(), answers.end()); for (int i = 0; i < answers.size(); i++) { cout << answers[i] + 1 << " "; } return 0; } | cs |