Easy is Perfect

[백준] 14003번 C/C++ 풀이 _ 가장 긴 증가하는 부분 수열 5

  • melonicedlatte
  • Jul 16, 2018


- 출처 : https://www.acmicpc.net/problem/14003 

가장 긴 증가하는 부분 수열 5  스페셜 저지

시간 제한메모리 제한제출정답맞은 사람정답 비율
3 초512 MB97037726646.503%

문제

수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.

예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.

입력

첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다.

둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000)

출력

첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.

둘째 줄에는 정답이 될 수 있는 가장 긴 증가하는 부분 수열을 출력한다.

예제 입력 1 

6
10 20 10 30 20 50

예제 출력 1 

4
10 20 30 50

출처

비슷한 문제

- 풀이방법

http://melonicedlatte.com/2018/07/15/171956.html 가 바로 전 단계의 문제 풀이입니다. 


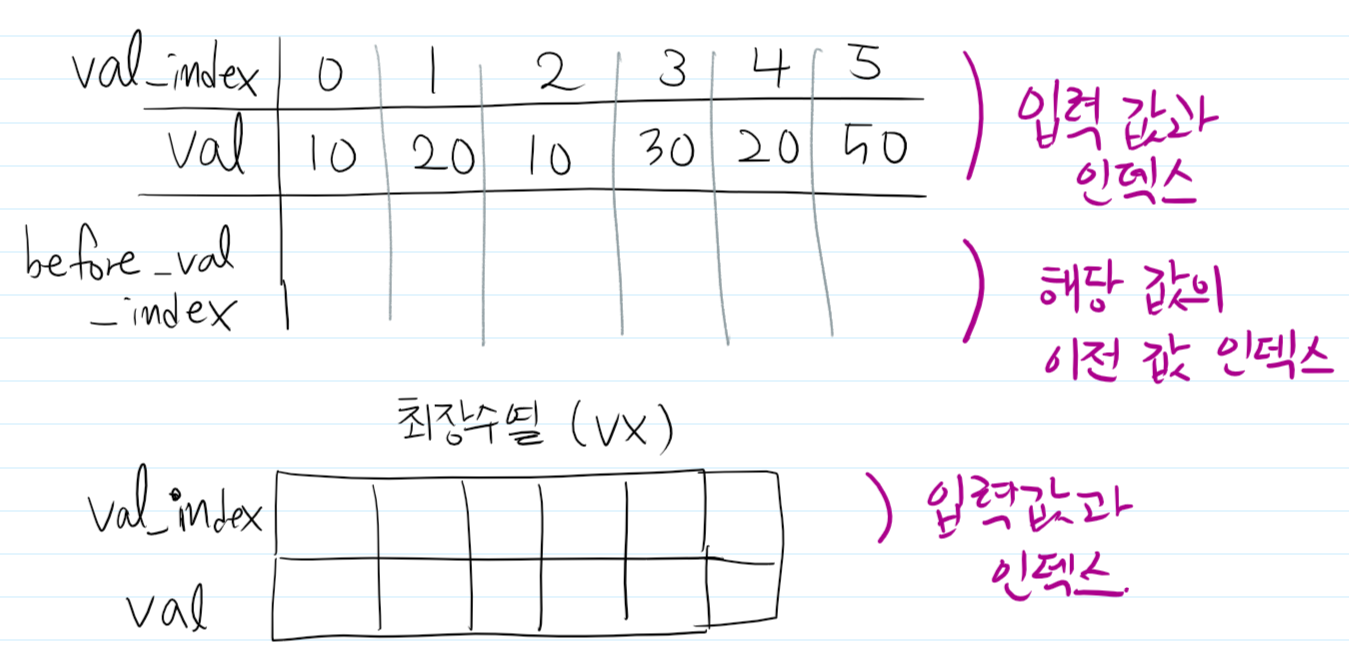
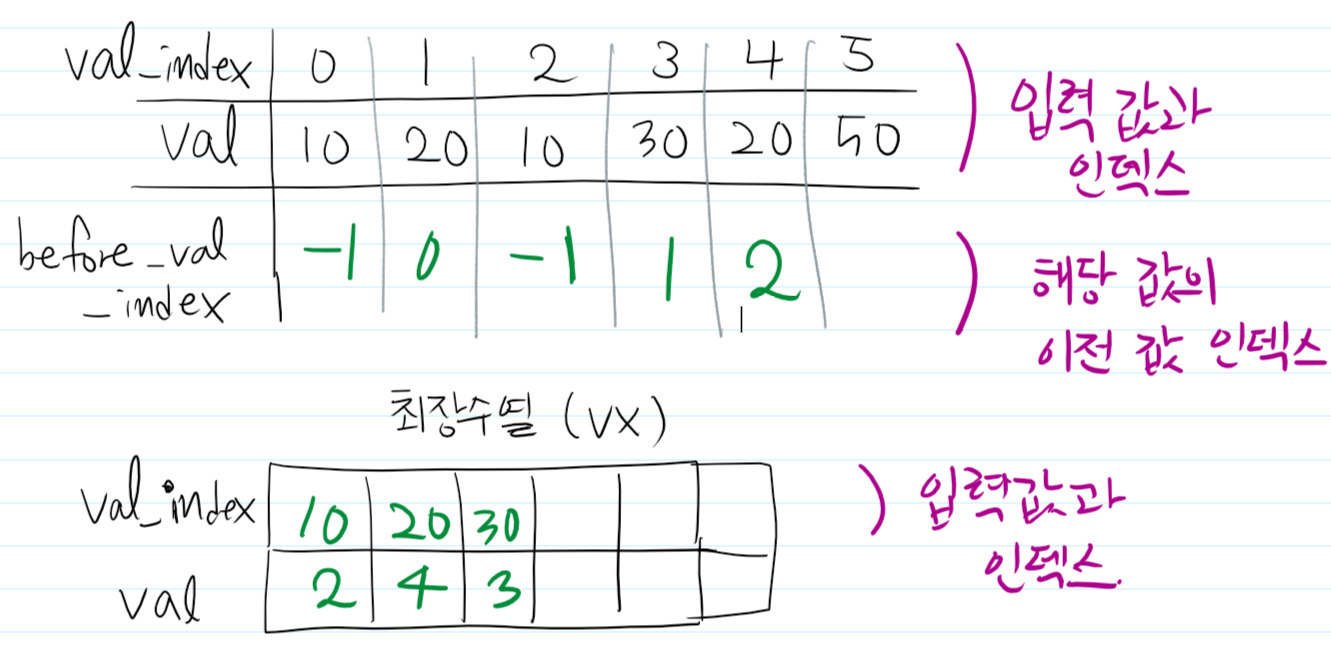
위의 행렬은 입력받은 값을 순차적으로 저장한 행렬입니다. 
val은 값, val_index는 해당 행렬에서의 값의 인덱스입니다. 

최장수열은 값과 인덱스를 함께 저장합니다. 

그리고 최장 수열을 지속해서 갱신하나가면서, before_val_index 라는 녀석도 넣어주어야 합니다.
최장 수열에서의 해당 값의 위치의 '전'에 들어간 값의 인덱스를 넣어줍니다. 

최장 수열에서는 행렬이 정답 행렬이라는 것을 보장하지는 않지만 '마지막 값'이 정답 행렬의 '마지막 값'이라는 것은 보장되어 있습니다.

그래서 vx 에서의 최대 값을 찾아낸 다음, 이전 값들로 계속해서 넘어가서 정답을 찾아내는 방식입니다.


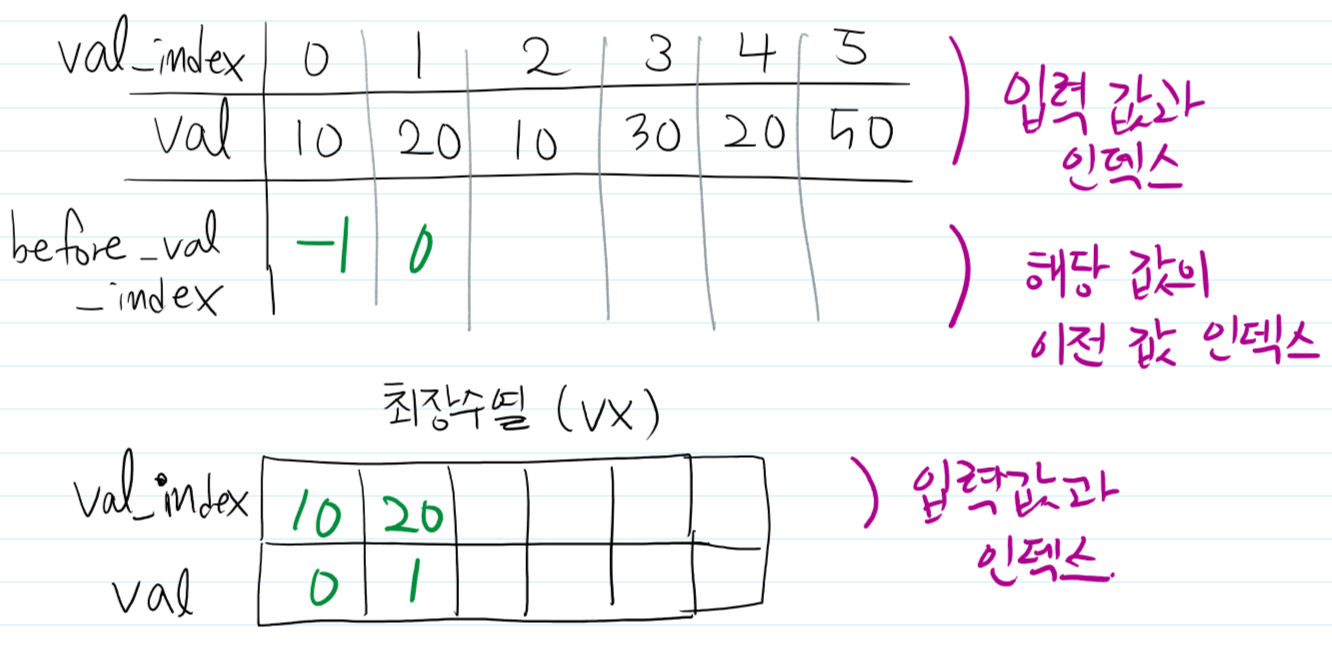
먼저, 10과 20을 표현해줍니다. 
10은 맨 처음의 수이기 때문에 before_val_index에 -1을 넣어줍니다. 

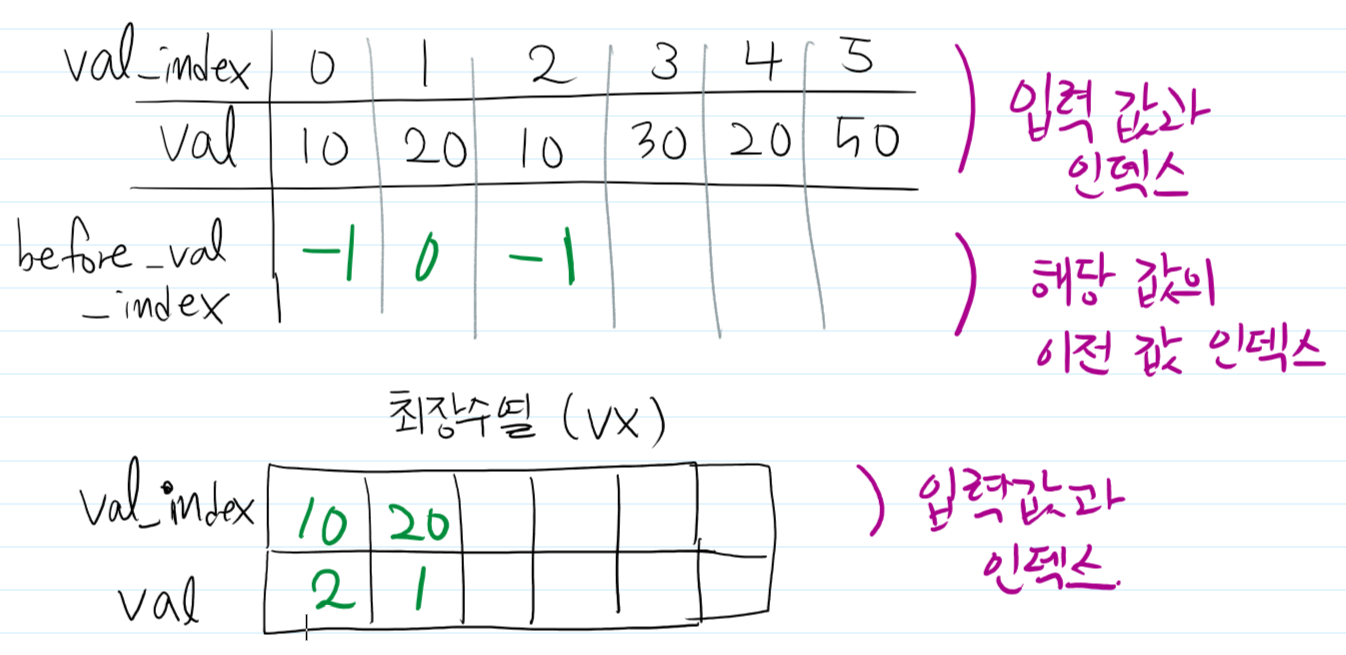
그 다음으로는 10을 넣어줘서 갱신하면 최장 수열의 맨 앞에 오기 때문에 위와 같이 표기됩니다. 

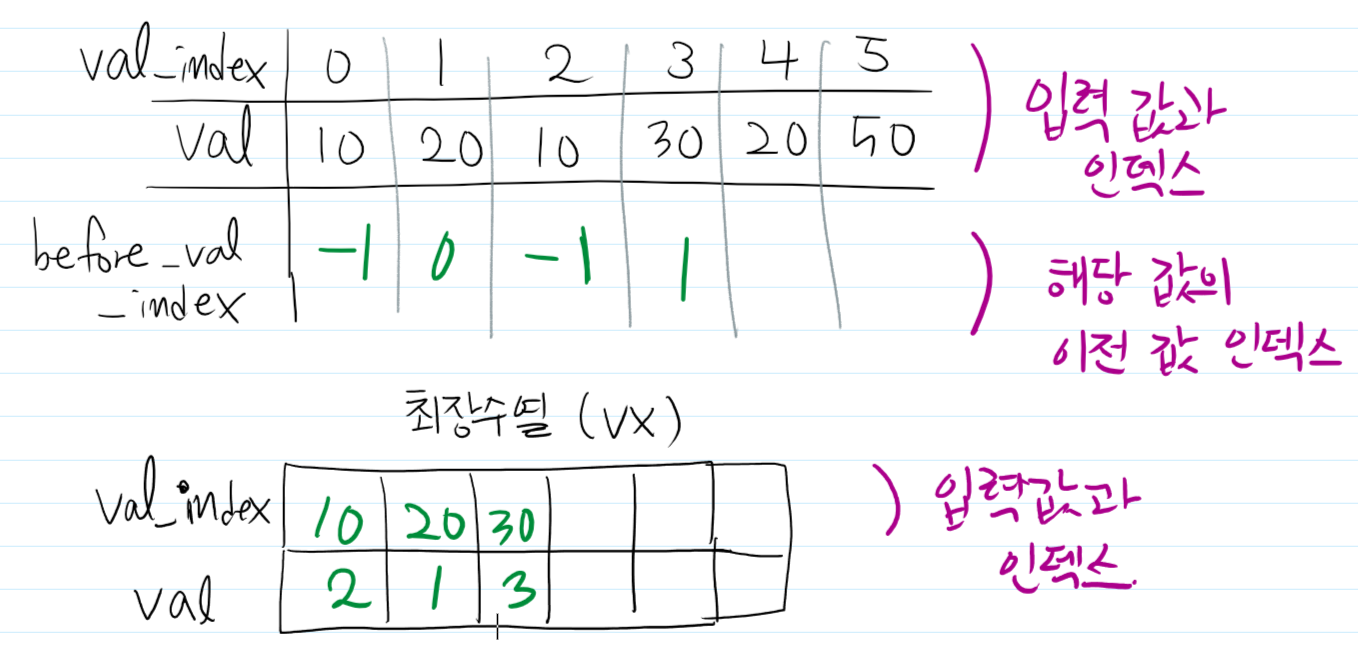
다음으로는 30을 넣어주고, 값을 갱신합니다.



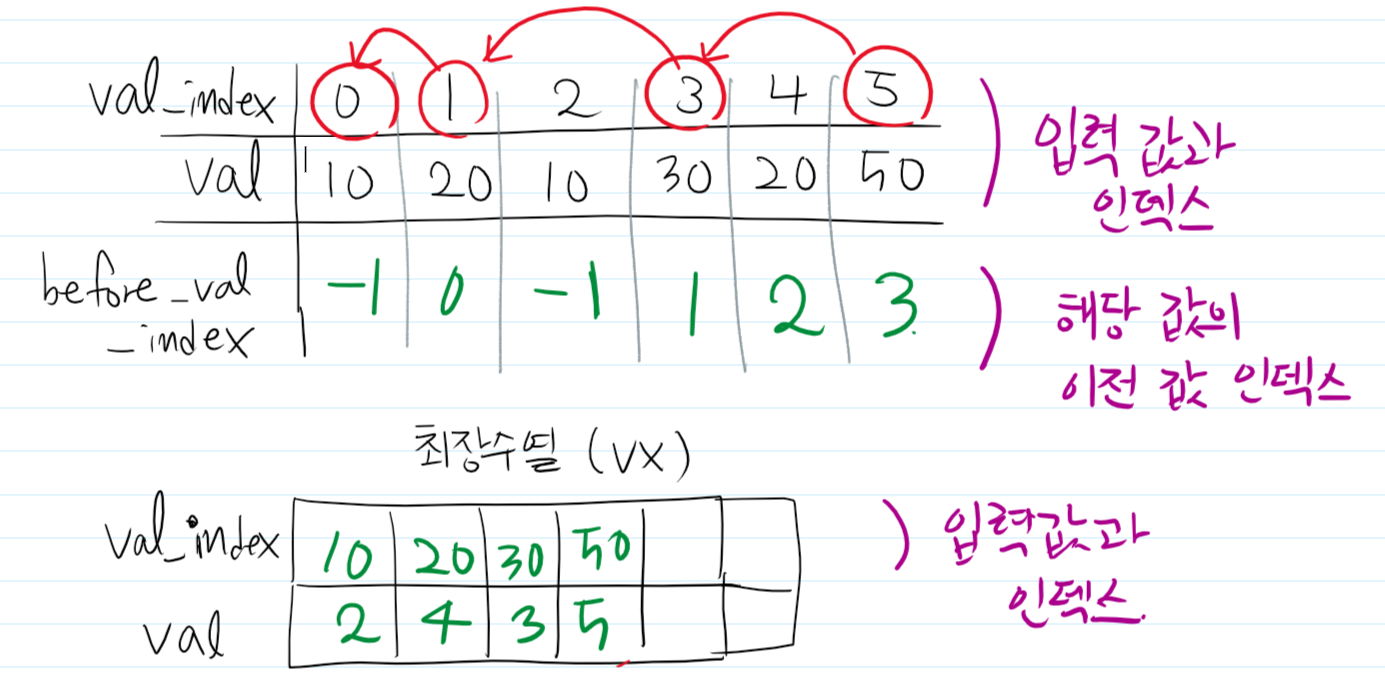
값을 모두 갱신하면 위와 같습니다. 

최장 수열의 마지막 값에서 before_val_index 를 추적하면 정답이 나오게 됩니다. 

아래는 다른 예시를 글로 써 본 것입니다. (위치랑 용어가 약간 상이한데 이해하는데는 무리 없으실 겁니다. )


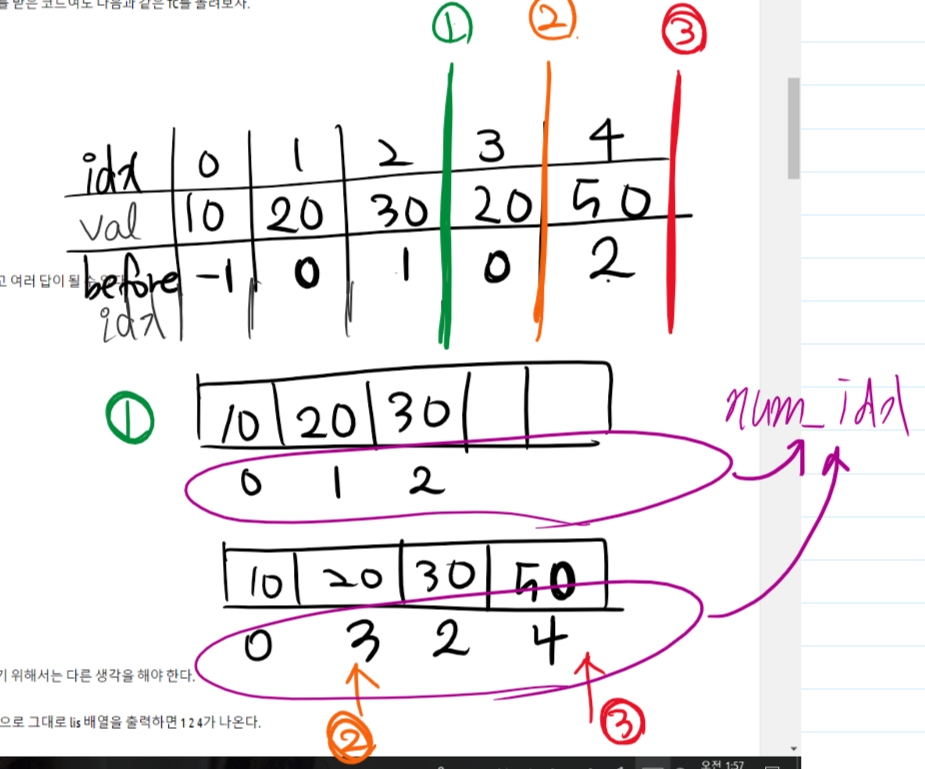
http://www.crocus.co.kr/681 같은 풀이인데 참고해보세요. 

- 소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<iostream>
#include<algorithm>
#include<vector>
#include<iterator>
using namespace std;
 
vector<int> vt;
vector<int> vt_index;
vector<int> num_vec;
vector<int> before_vector;
vector<int>::iterator iter; 
 
int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(0);
 
    int n, data;
 
    cin >> n;
    before_vector.resize(n);
    for (int i = 0; i < n; i++) {
        cin >> data;
        num_vec.push_back(data);
        if (i == 0) {
            vt.push_back(data);
            before_vector.at(i) = -1;
            vt_index.push_back(i); 
        }
 
        if (vt.back() < data) {
            vt.push_back(data);
            before_vector.at(i) = vt_index.back();
            vt_index.push_back(i);
        }
        else {
            iter = lower_bound(vt.begin(), vt.end(), data);
            *iter = data;
            int now_index = iter - vt.begin();
            if (now_index > 0)
                before_vector.at(i) = vt_index.at(now_index -1);
            else
                before_vector.at(i) = -1;
            vt_index.at(now_index) = i;
        }
    }
     
    cout << vt.size() << endl;
 
    int print_index = vt_index.back();
    vector<int> ans_vec;
    while (print_index != -1) {
        ans_vec.push_back(num_vec.at(print_index) );
        print_index = before_vector.at(print_index);
    }
 
    sort(ans_vec.begin(), ans_vec.end());
 
    for (int ans_idx = 0; ans_idx < ans_vec.size(); ans_idx++)
        cout << ans_vec.at(ans_idx) << " ";
 
    return 0;
 
}
cs



Search