Easy is Perfect

[백준] 2632번 C/C++ 풀이 _ 피자판매

  • melonicedlatte
  • Aug 29, 2018


출처 : https://www.acmicpc.net/problem/2632

피자판매 성공

시간 제한메모리 제한제출정답맞은 사람정답 비율
2 초128 MB86630522536.946%

문제

고객이 두 종류의 피자 A와 B를 취급하는 피자가게에서 피자를 주문하고자 한다. <그림 1>과 같이 각 종류의 피자는 다양한 크기의 여러 개의 피자조각으로 나누어져 있다. 각 조각에 쓰여진 숫자는 피자조각의 크기를 나타낸다.

고객이 원하는 피자의 크기를 이야기하면, 피자가게에서는 한 종류의 피자를 2 조각 이상 판매할 때는 반드시 연속된 조각들을 잘라서 판매한다. 이때 판매한 피자조각의 크기 합이 주문한 크기가 되어야 한다. 판매한 피자조각은 모두 A종류이거나, 모두 B종류이거나, 또는 A와 B 종류가 혼합될 수 있다. 예를 들어서, <그림 1> 과 같이 잘라진 피자가 있을 때, 손님이 전체 크기가 7 인 피자를 주문하면, 피자 가게에서는 <그림2>와 같이 5 가지 방법으로 피자를 판매할 수 있다.

피자가게에서 손님이 원하는 크기의 피자를 판매하는 모든 방법의 가지 수를 계산하는 프로그램을 작성하시오

입력

첫 번째 줄에는 손님이 구매하고자 하는 피자크기를 나타내는 2,000,000 이하의 자연수가 주어진다. 두 번째 줄에는 A, B 피자의 피자조각의 개수를 나타내 는 정수 m, n 이 차례로 주어진다 ( 3≤m, n≤1000). 세 번째 줄부터 차례로 m 개의 줄에는 피자 A의 미리 잘라진 피자조각의 크기를 나타내는 정수가 주어진다. 그 다음 n 개의 줄에는 차례로 피자B의 미리 잘라진 피자조각의 크기를 나타내는 정수가 주어진다. 각 종류의 피자조각의 크기는 시계방향으로 차례로 주어지며, 각 피자 조각의 크기는 1000 이하의 자연수이다.

출력

첫째 줄에는 피자를 판매하는 방법의 가지 수를 나타내는 정수를 출력한다. 피자를 판매하는 방법이 없는 경우에는 숫자 0을 출력한다.

예제 입력 1 

7
5 3
2
2
1
7
2
6
8
3

예제 출력 1 

5

출처

Olympiad > 한국정보올림피아드 > KOI 2001 > 중등부 3번

풀이

저는 이 문제를 풀 때, 먼저 '구간 합을 저장하는 배열을 만들자' 라는 생각을 했습니다. 


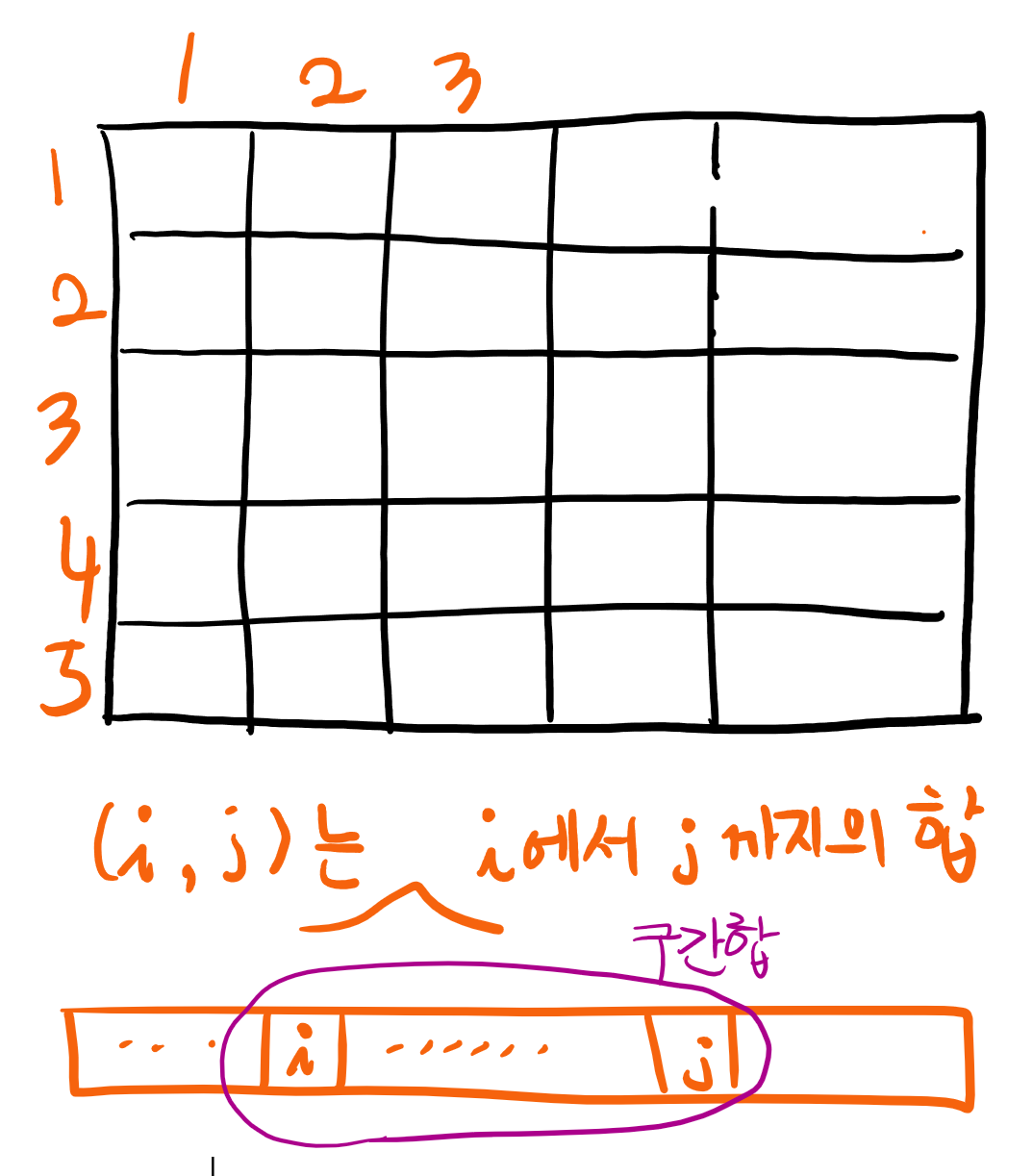
(i,j) 는 입력받은 피자의 순서대로 i에서 j까지의 피자의 합입니다.
N, M 이 1000 이기 때문에 N2 M2 를 구하더라 하더라도 시간초과가 나지 않습니다. 

풀다가 한 가지 문제가 생겼습니다.
피자는 둥그런 모양이기 때문에, 뒤에 있는 인덱스에서 부터 앞에 있는 인덱스끼리의 합도 존재할 수 있습니다. 

2 2 1 7 과 같은 순서대로 들어 오더라도 7 2 2 와 같은 순서대로 피자를 연속해서 손님에게 줄 수 있습니다.
즉, j~i 까지의 합도 구해주어야합니다. (가령, 4번째 인덱스 부터 2번째 인덱스 까지)

j~i 까지의 합은 0~n-1 까지의 인덱스의 합에서 i+1 ~ j-1 까지의 합을 빼주면 됩니다. 

이렇게 구한 행렬 값을 기준으로 존재하는 숫자를 map 에 넣었습니다.
배열에 넣어도 되지만 map 이 더 빠르다고 판단해서 map 에 넣었습니다. 

존재하는 숫자의 숫자를 세주기 위하여 map에다가 행렬에 있는 숫자를 세서 넣어주었습니다. 

그리고 소비자가 원하는 피자의 값을 만족시키는 값(want_size) 를 x, y 로 나눠서 각각의 map 에서 값이 존재하는지 확인합니다. 

만약, 두 곳의 값이 존재한다면 map_a[x] * map_b[y] 를 정답에 추가해줍니다. 
이는 a 에서 연속한 피자들로 x를 만들 수 있는 개수 * b 에서 연속한 피자들로 y 를 만들 수 있는 개수 입니다. 

양 끝점에서는 각각 a와 b의 값을 정답에 더해줍니다. 

자세한 풀이는 소스코드를 참조해주세요~

소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <iostream>
#include <map>
#include <vector>
using namespace std;
 
// 행렬 만들어주기 
void make_matrix(vector<vector<int>>& _pizza_mat, vector<int>& _pizza_vec, int _size) { 
    // 오른쪽 위 행렬 갱신 
    for (int r_idx = 0; r_idx < _size; r_idx++) {
        for (int c_idx = r_idx; c_idx < _size; c_idx++) {
            // 만약, 대각선에 위치한 원소이면 해당 원소의 값을 넣어준다. 
            if (r_idx == c_idx) {
                _pizza_mat[r_idx][c_idx] = _pizza_vec[c_idx];
                continue;
            }
            // 아니면 이전 행렬의 값에서 + 배열에서의 현재 추가되어야 할 인덱스의 값 
            _pizza_mat[r_idx][c_idx] = _pizza_mat[r_idx][c_idx - 1] + _pizza_vec[c_idx];
        }
    }
    // 왼쪽 아래 행렬 갱신 
    for (int r_idx = 0; r_idx < _size; r_idx++)
        for (int c_idx = 0; c_idx < r_idx -1 ; c_idx++) 
            if (c_idx + 1 <= r_idx - 1)
                _pizza_mat[r_idx][c_idx] = _pizza_mat[0][_size - 1] - _pizza_mat[c_idx + 1][r_idx - 1];
 
}
 
// 피자에 구간 합으로 가능한 경우의 수를 값에 따라서 몇 개인지 센다.
// ex) 구간합이 7인 것의 개수가 행렬에서 몇 개인지 구한다. 
void make_map(vector<vector<int>>& _pizza_mat, map<int, int>& _pizza_map, int _size){
    for (int r_idx = 0; r_idx < _size; r_idx++) {
        for (int c_idx = 0; c_idx < _size; c_idx++) {
            int now_mat_val = _pizza_mat[r_idx][c_idx];
            // 값이 없으면?
            if (_pizza_map.find(now_mat_val) == _pizza_map.end())
                _pizza_map[now_mat_val] = 1;
            else
                _pizza_map[now_mat_val]++;
        }
    }
}
 
int main() {
    int want_size, M, N;
    cin >> want_size >> M >> N;
    vector<int> pizza_vec_a(M);
    vector<int> pizza_vec_b(N);
    
    // input 
    for (int m_idx = 0; m_idx < M; m_idx++)
        cin >> pizza_vec_a.at(m_idx);
    for (int n_idx = 0; n_idx < N; n_idx++)
        cin >> pizza_vec_b.at(n_idx);
 
    // 구간 합 행렬 만들기 
    // i 행 j열 원소는 i~j 까지의 합을 의미한다. 
    vector<vector<int>> pizza_mat_a(M, vector<int>(M,0));
    vector<vector<int>> pizza_mat_b(N, vector<int>(N,0));
 
    make_matrix(pizza_mat_a, pizza_vec_a, M);
    make_matrix(pizza_mat_b, pizza_vec_b, N);
 
    // 행렬을 탐색하면서 해당 값을 맵에 저장 
    map<int, int> pizza_map_a;
    map<int, int> pizza_map_b;
 
    make_map(pizza_mat_a, pizza_map_a, M);
    make_map(pizza_mat_b, pizza_map_b, N);
 
    // 원하고자 하는 피자의 크기를 토대로 가능한 A와 B에서의 크기를 
    // map 에서 찾아서 두 개 다 0이 아닌 경우에 정답에 두 수의 곱을 추가한다. 
    int answer_num = 0;
    for (int a_size = 0; a_size <= want_size; a_size++) {
        int b_size = want_size - a_size; 
        // 양끝점 다르게 처리 
        if (a_size == 0){
            if(pizza_map_b.find(b_size) != pizza_map_b.end())
                answer_num += pizza_map_b[b_size]; 
            continue;
        }
        if (b_size == 0) {
            if(pizza_map_a.find(a_size) != pizza_map_a.end())
                answer_num += pizza_map_a[a_size];
            continue;
        }
 
        // 두 피자의 값이 둘 다 존재하면 정답에 추가 
        if (pizza_map_a.find(a_size) != pizza_map_a.end() &&
            pizza_map_b.find(b_size) != pizza_map_b.end())
            answer_num += pizza_map_a[a_size] * pizza_map_b[b_size];
    }
 
    cout << answer_num; 
 
    return 0; 
}
cs



Search