[프로그래머스] 멀쩡한 사각형 풀이

1. 문제

https://programmers.co.kr/learn/courses/30/lessons/62048#

2. 풀이 방법

x 좌표를 1씩 증가시키면서 x+1 에서의 y 값 올림 - x에서의 y 값 내림 방법으로 문제 해결 후 실패 및 해설 참조
왼쪽 상단과 오른쪽 하단의 꼭지점 2개를 직선을 가지는 최소 크기의 사각형을 구해야 문제 해결 가능. 이를 위하여 gcd를 구함.

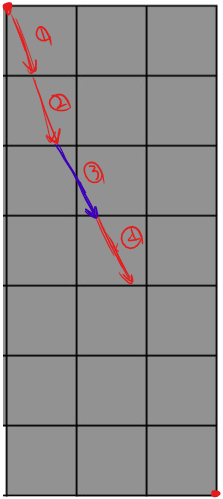왼쪽 상단과 오른쪽 하단의 꼭지점 2개를 지나는 직선을 포함한 최소 크기의 직사각형

왼쪽 상단과 오른쪽 하단의 꼭지점 2개를 지나는 직선은 항상 높이 + 너비 - 1 만큼의 사각형을 지난다. 이유는 아래와 같다.
- 높이가 항상 너비보다 크다고 가정해보자. 1,2번과 같은 상황에서는 직선이 지나가면서 x값이 증가하면서 y축에 있는 선들을 지나가지 않는다. 이 때에는 높이가 줄어드는 크기만큼 증가한다.
- 3번과 같은 상황에서는 높이가 줄어드는 크기 + 1 이 된다. 이러한 상황이 너비 -1 번 만큼 발생한다. 따라서, 항상 지나는 사각형의 개수는 높이 + 너비 - 1이다.

3. 소스코드

3.1. 숏코딩 by programmers

def gcd(a, b):
    return b if a % b == 0 else gcd(b, a % b)

def solution(w, h):
    whole = w * h;
    broken = w + h - gcd(w, h)
    return whole - broken

3.2. 실패한 소스코드

시간 복잡도는 O(n)으로, x 좌표를 1씩 증가시키면서 x+1 에서의 y 값 올림 - x에서의 y 값 내림 방법으로 문제 해결 후 실패

import math 

def func(w, h, x):
    return (h/w)*(x)

def solution(w,h):
    answer = 0 
    if w > h:
        w, h = h, w
    
    for i in range(w):
        answer += math.ceil(func(w, h, i+1)) - math.floor(func(w, h, i))
        print(math.ceil(func(w, h, i+1)) , math.floor(func(w, h, i)))
    return h*w - answer

테스트 케이스에서 시간 초과 및 실패 발생. 아래와 같은 원인 때문으로 추측(by jandy14님의 질문/답변)

접근법은 좋은거 같습니다. 논리적인 오류도 없구요.
실패가 뜨신 이유는 실수값 오차로 인해서 생긴거 같아요.
그런 케이스를 찾지는 못했지만 fraction으로 계산해 실행시킬땐 4번케이스가 정답이었습니다. 실수값 오차에 대해서는 제가 설명하는 것보다는 직접 찾아보시는게 좋을거 같아요. https://dojang.io/mod/page/view.php?id=2466 시간초과는 다른 방법과 비교해보면, 최대공약수를 이용해서 불완전한 사각형을 찾는 방법은 (h / 최대공약수) 만큼만 계산하는 반면, 위 방법은 어떤 경우든 h만큼 계산해야하는 차이가 있습니다.
이 차이로 인해 시간초과가 뜬것이 아닐까합니다. 늦은 답변이지만 혹시 도움이 될까해서 올립니다.

아래와 같은 방법으로 정확도 보정 필요한 것으로 보여집니다.

>>> import math, sys
>>> x = 0.1 + 0.2
>>> math.fabs(x - 0.3) <= sys.float_info.epsilon
True

출처

https://dojang.io/mod/page/view.php?id=2466

PREVIOUSWhat is the python for-else? How to use?

NEXT[프로그래머스] 소수 찾기 풀이