출처 : https://www.acmicpc.net/problem/11066
파일 합치기 성공 풀이
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 256 MB | 4457 | 2328 | 1475 | 52.716% |
문제
소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을 합칠 때 필요한 비용(시간 등)이 두 파일 크기의 합이라고 가정할 때, 최종적인 한 개의 파일을 완성하는데 필요한 비용의 총 합을 계산하시오.
예를 들어, C1, C2, C3, C4가 연속적인 네 개의 장을 수록하고 있는 파일이고, 파일 크기가 각각 40, 30, 30, 50 이라고 하자. 이 파일들을 합치는 과정에서, 먼저 C2와 C3를 합쳐서 임시파일 X1을 만든다. 이 때 비용 60이 필요하다. 그 다음으로 C1과 X1을 합쳐 임시파일 X2를 만들면 비용 100이 필요하다. 최종적으로 X2와 C4를 합쳐 최종파일을 만들면 비용 150이 필요하다. 따라서, 최종의 한 파일을 만드는데 필요한 비용의 합은 60+100+150=310 이다. 다른 방법으로 파일을 합치면 비용을 줄일 수 있다. 먼저 C1과 C2를 합쳐 임시파일 Y1을 만들고, C3와 C4를 합쳐 임시파일 Y2를 만들고, 최종적으로 Y1과 Y2를 합쳐 최종파일을 만들 수 있다. 이 때 필요한 총 비용은 70+80+150=300 이다.
소설의 각 장들이 수록되어 있는 파일의 크기가 주어졌을 때, 이 파일들을 하나의 파일로 합칠 때 필요한 최소비용을 계산하는 프로그램을 작성하시오.
입력
프로그램은 표준 입력에서 입력 데이터를 받는다. 프로그램의 입력은 T개의 테스트 데이터로 이루어져 있는데, T는 입력의 맨 첫 줄에 주어진다.각 테스트 데이터는 두 개의 행으로 주어지는데, 첫 행에는 소설을 구성하는 장의 수를 나타내는 양의 정수 K (3 ≤ K ≤ 500)가 주어진다. 두 번째 행에는 1장부터 K장까지 수록한 파일의 크기를 나타내는 양의 정수 K개가 주어진다. 파일의 크기는 10,000을 초과하지 않는다.
출력
프로그램은 표준 출력에 출력한다. 각 테스트 데이터마다 정확히 한 행에 출력하는데, 모든 장을 합치는데 필요한 최소비용을 출력한다.
예제 입력
2 4 40 30 30 50 15 1 21 3 4 5 35 5 4 3 5 98 21 14 17 32
예제 출력
300 864
힌트
출처
ACM-ICPC > Regionals > Asia > Korea > Nationwide Internet Competition > Asia Regional - Daejeon Nationalwide Internet Competition 2015 F번
>> 문제 풀이
이 문제는 다이나믹 프로그래밍으로 풀어야 하는 문제이다.
처음에는 인접한 2개만 합쳐야되는지 모르고, 가장 최소로 합치는 풀이만 진행했다.
사실 인접한 2개인지 알았어도 틀렸을 것 같다.
다이나믹프로그래밍에는 아직 한참 멀은 것 같다.
전혀 답이 떠오르지 않아서 답을 보고 말았다.
답을 보고도 해설을 엄청나게 오랫동안 보았다.
갈 길이 멀다.
해당 문제에 대해서 매우 자세히 서술해 놓은 블로그가 있어서 아래 출처를 남기고 참고를 많이 하여 포스팅한다.
종신1재정2시경3 이라는 블로그이다.
문제 풀이는 최단 거리를 구하는 방법을 모든 방법을 탐색하여 값을 얻는 것도 좋지만
문제에서 적용 가능한 매우 빠른 방법으로 찾는 것도 좋다.
전자의 경우 안되는 문제는 후자로 풀라고 내는 문제가 대다수 인 것 같고,
후자의 경우는 알기 힘들거나 틀리는 경우가 대다수이기 때문에 전자가 '오래 걸리더라도 답은 무조건 나오는' 풀이인 것 같다.
무튼 이 문제도 전자, 즉 '최단거리를 구하는 방법을 모두 탐색하여 가장 최소값을 찾는다.' 라는 마인드를 기반으로 들어간다.
[a, b] 구간의 최소 합을 구하기 위해서는 [a,k] [k+1,b] 구간의 최소 합을 구해서 더하는 것이 가장 중요한 내용이다.
풀이 1
>> 해설
이 풀이는 해당 블로그의 2번 풀이이다.
기존에 많이 사용하는 재귀함수를 사용해서 처음 보았을 때, 가장 친숙했다.
dp[a][b] 배열의 값은 a에서 b 구간까지의 최소합을 의미한다.
그리고 dp[a][a] = 0 이면 끝이라고 생각하고 0을 리턴하고 종료하고,
dp[a][a+1] = cost[a]+cost[a+1] (a부터 a+1 의 값을 채우는 최소값) 이다.
sum 배열은 1~i번째 인덱스 까지의 합이다.
아래의 알고리즘은 재귀함수에 시작점과 끝점을 넣어서 계속 분할하여 최소값이면 dp배열에 넣는다.
아래와 같은 구조로 이루어진다.
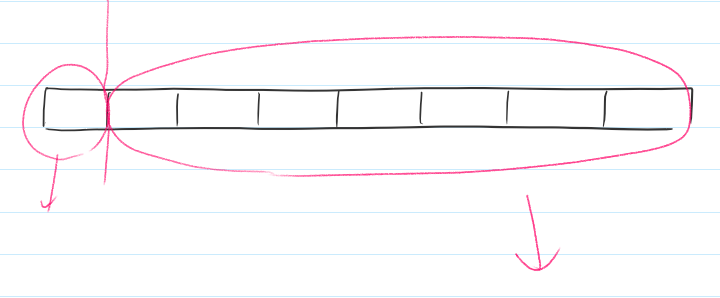
전체 구간이 8개라고 가정해보자.
첫 재귀함수를 호출하는 구간에서는 아래와 같이 각 구간의 최솟값을 구하는 재귀함수를 다시 호출한다.
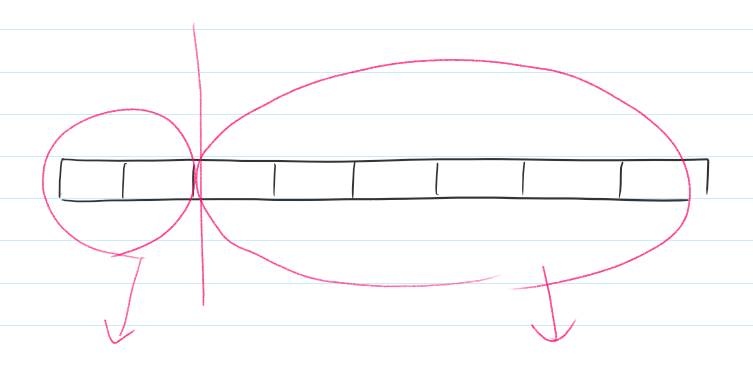
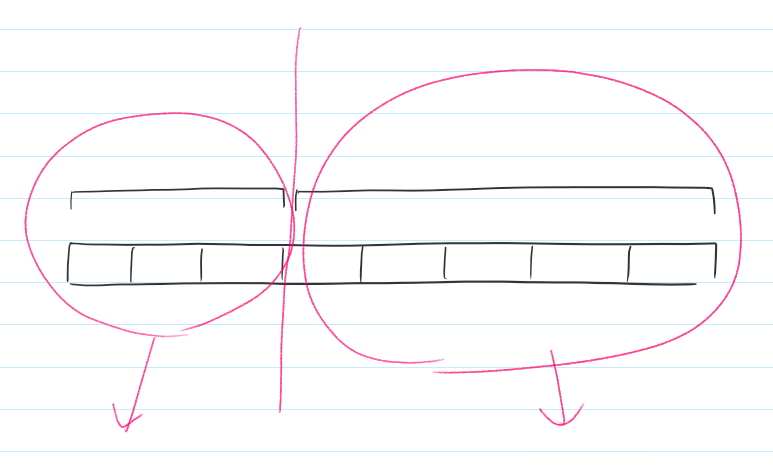
해당 재귀함수들이 또 다시 재귀함수들을 호출한다.
지속적으로 반복된다.
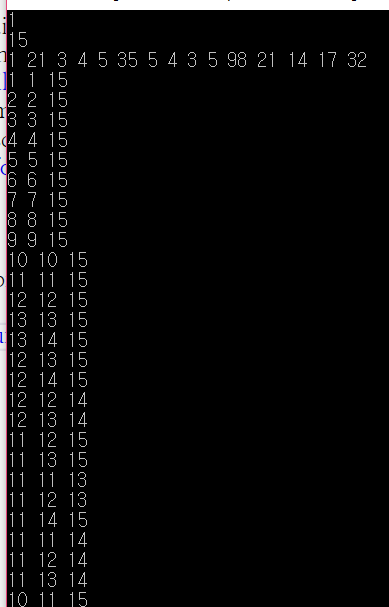
실제 예제를 출력해보면 아래와 같다.
처음 값은 tx, 중간 값은 mid, 끝 값은 ty 이다.
>> 소스코드
37줄 : 1~i 번 까지의 합인 sum[i] 값 넣기
11~28줄 : tx에서 ty까지의 최소값을 구하는 dpf 함수를 정의한다.
15줄 : tx와 ty가 같으면 0을 리턴
18줄 : tx와 ty가 1차이가 나면 cost[tx]+cost[ty]를 리턴한다(2개의 인접한 종이를 합치는 값)
21줄 : tx와 ty사이의 값을 mid로 지정하고, for 문을 돌면서 mid를 1씩 증가시키면서 재귀함수를 호출한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #include <stdio.h> #include <string.h> #include <algorithm> using namespace std; int dp[501][501]; int cost[501]; int sum[501]; int t, k, i; int dpf(int tx, int ty) { if (dp[tx][ty] != 0x3f3f3f3f) return dp[tx][ty]; if (tx == ty) return dp[tx][ty] = 0; if (tx + 1 == ty) return dp[tx][ty] = cost[tx] + cost[ty]; for (int mid = tx; mid < ty; ++mid) { int left = dpf(tx, mid); int right = dpf(mid + 1, ty); dp[tx][ty] = min(dp[tx][ty], left + right); } return dp[tx][ty] += sum[ty] - sum[tx - 1]; } int main() { scanf("%d", &t); while (t--) { memset(dp, 0x3f, sizeof(dp)); scanf("%d", &k); for (i = 1; i <= k; ++i) { scanf("%d", &cost[i]); sum[i] = sum[i - 1] + cost[i]; } printf("%d\n", dpf(1, k)); } return 0; } | cs |
풀이 2
>> 해설
소스코드만 보면 이해가 잘 되지 않는다.
먼저, sum[k] 는 1번부터 k번째까지의 숫자를 전부 더한 값이다.
아래의 그림을 보면서 함께 이해해보자.
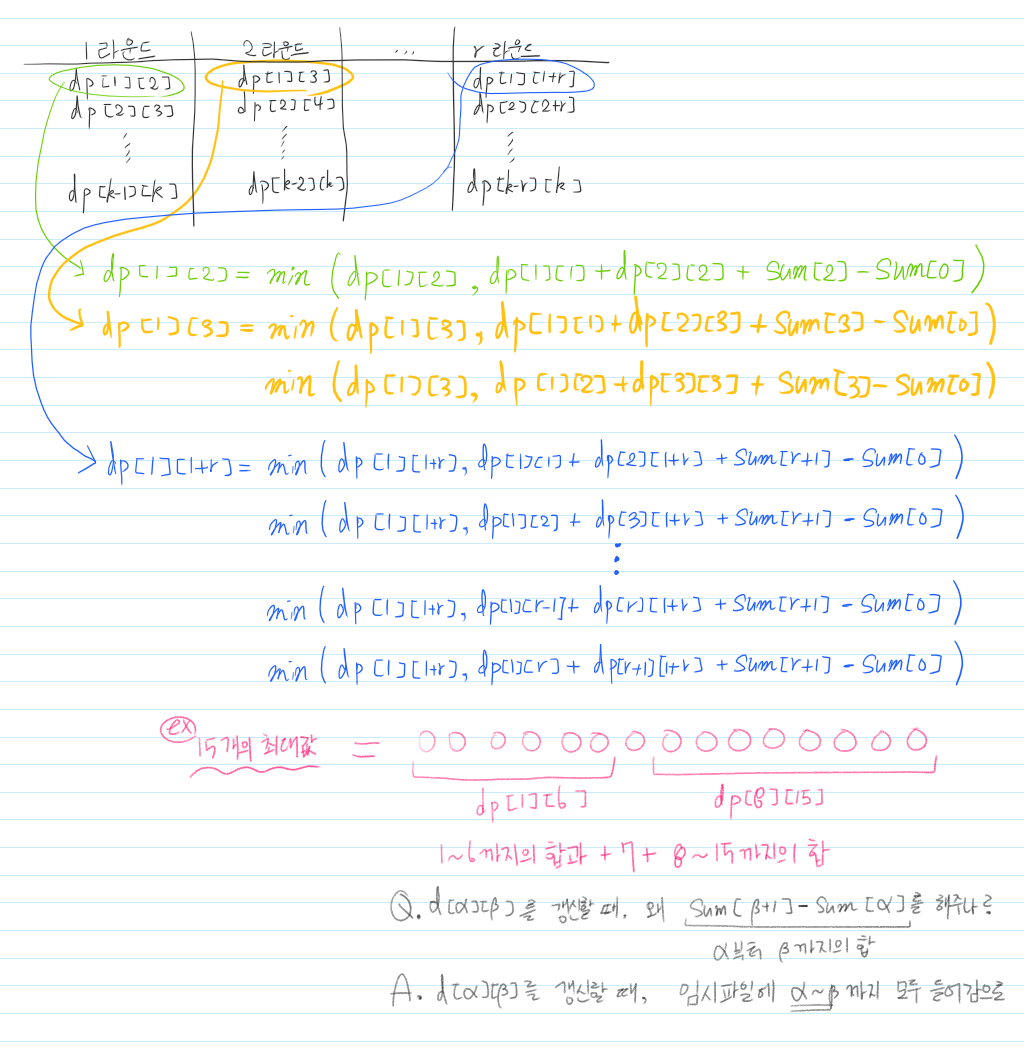
먼저 1라운드에는 dp[a][a+1]꼴을 전부 갱신한다.
아래를 보면 dp[1][2], dp[2][3] ..... 을 수행하는 것을 알 수 있다.
dp[1][2] = min(dp[1][2], dp[1][1]+dp[2][2] + sum[2]-sum[0])
다음 2라운드에는 dp[a][a+1]꼴을 전부 갱신한다.
아래를 보면 dp[1][3], dp[2][4] ..... 을 수행하는 것을 알 수 있다.
dp[1][3] = min(dp[1][3], dp[1][1]+dp[2][3] + sum[3]-sum[0])
or min(dp[1][3], dp[1][2]+dp[3][3] + sum[3]-sum[0])
계속해서 나열하면 다음과 같은 규칙을 얻을 수 있다.
다음 r라운드에는 dp[a][a+r]꼴을 전부 갱신한다.
아래를 보면 dp[1][1+r], dp[2][2+r] ..... 을 수행하는 것을 알 수 있다.
dp[1][1+r] = min(dp[1][1+r], dp[1][1]+dp[2][1+r] + sum[r+1]-sum[0])
or min(dp[1][1+r], dp[1][2]+dp[2][1+r] + sum[r+1]-sum[0])
or ........
or min(dp[1][1+r], dp[1][r]+dp[1+r][1+r] + sum[r+1]-sum[0])
즉, 라운드가 증가할 때마다 갭이 큰 구간을 모두 갱신해주는 것이다.
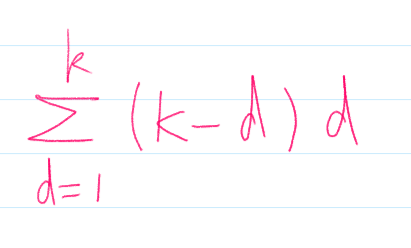
총 시간 복잡도는 위와 같은 식이 나오게 되고, 때문에 k=N이라고 보면 O(N3)이 된다.
>> 소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | #include <stdio.h> #include <string.h> #include <limits.h> #include <algorithm> using namespace std; int dp[501][501]; int cost[501]; int sum[501]; int t, k, i; int main() { scanf("%d", &t); while (t--) { scanf("%d", &k); for (i = 1; i <= k; ++i) { scanf("%d", &cost[i]); sum[i] = sum[i - 1] + cost[i]; } for (int d = 1; d < k; ++d) { for (int tx = 1; tx + d <= k; ++tx) { int ty = tx + d; dp[tx][ty] = INT_MAX; for (int mid = tx; mid < ty; ++mid) dp[tx][ty] = min(dp[tx][ty], dp[tx][mid] + dp[mid + 1][ty] + sum[ty] - sum[tx - 1]); } } printf("%d\n", dp[1][k]); } return 0; } | cs |
풀이 3
>> 해설
풀이 1은 580ms, 풀이 2는 120ms 내외의 값을 가진다고 한다.
풀이 1은 재귀함수이기 때문에 stack에 복귀 주소를 넣어서 여러번 함수를 호출 하는 형태이기 때문에 느릴 수 밖에 없다.
Kruth's optimization 알고리즘을 사용하면 20ms 정도가 나온다고 한다.
이 알고리즘을 사용하면 위에서 구한 값과 다르게 O(N2)를 가진다.
해당 알고리즘에 대한 설명은 해당 블로그의 포스팅을 그대로 가져왔다.
Kruth's optimization의 정의
1) 사각부등식
C[a][c]+C[b][d]<=C[a][d]+C[b][c] (a<=b<=c<=d)
2) 단조증가
C[b][c]<=C[a][d] (a<=b<=c<=d)
위 두 조건을 만족하는 C[][]에 대해,
점화식이 dp[i][j] = min(i < k < j){dp[i][k] + dp[k][j]} + C[i][j] 꼴이라 하자.
이 때, num[i][j]란 dp[i][j]가 최소가 되게 하는 k(i < k < j)값을 저장하는 배열이라 정의하면, 다음이 성립한다.
num[i][j-1] <= num[i][j] <= num[i+1][j]
풀이 1에선 i부터 j까지의 모든 k에 대해 최소값을 구하느라 O(N^3)이 걸렸지만,
실제로는 정답인 k가 저 좁은 범위안에 있기 때문에 모든 k를 살펴볼 필요가 없으므로 최적화가 O(N^2)로 가능하다는 이론이다.
증명은 다음페이지를 참조하자.
http://www.egr.unlv.edu/~bein/pubs/knuthyaotalg.pdf
실제로 최적화가 적용가능한지 살펴보기 위해, 먼저 우리의 psum[][] 배열이 C[][] 꼴 인지 생각해보자.
1) 사각부등식에 대해, 앞의 항과 뒤의 항 모두 b~c의 novel[][]를 중복해서 더하므로, 등호를 만족한다.
2) 단조증가에 대해, psum[b][c]<=psum[a][d] 임은 자명하다.
다음으로 점화식에 대해 생각해보면, 우리의 점화식은 다음과 같았다.
i<=k<j인 k에 대해,
dp[i][j] = min(i <= k < j){dp[i][k] + dp[k+1][j]} + psum[i][j] -> i부터 j까지의 최소합비용
이제 Kruth's optimization을 적용하기 위해, 점화식을 수정해주자.
i<k<j인 k에 대해,
dp2[i][j] = min(i < k < j){dp2[i][k] + dp2[k][j]} + psum[i][j] -> i + 1부터 j까지의 최소합비용 (차이점에 주목하자)
점화식이 조금 수정되었지만, dp[i][j] = dp2[i-1][j] 이기 때문에 여전히 같은 기능을 수행한다.
정답은 dp2[0][N]을 출력하면 된다.
d=2 부터, i=0 부터 시작하는 것을 주의하라.
해당 설명을 읽어도 이해가 잘 되지 않아서, 코드 위에 펜으로 써보았다.
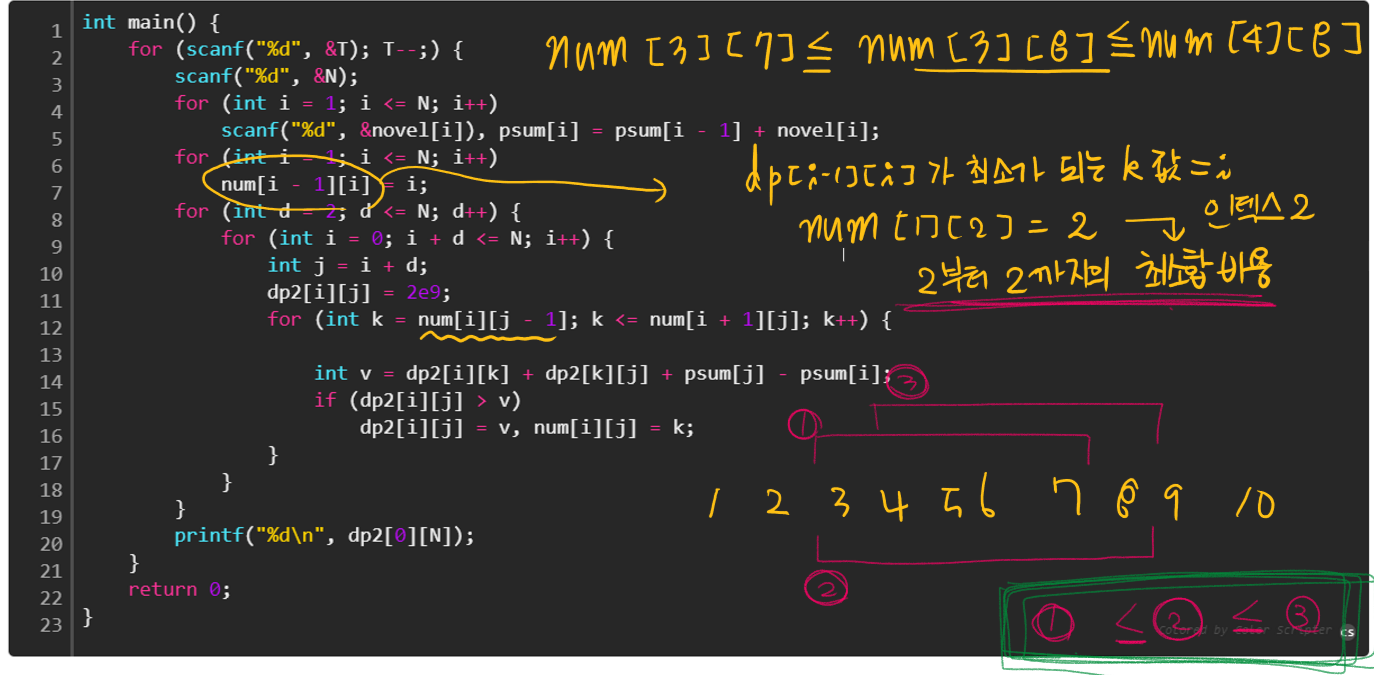
가령 구하고자 하는 구간이 d[3][8] 이라고 하면, num[3][8]은 최소합 비용을 구하는 인덱스를 가리킨다.
위의 증명에 따라서 나열해보면 아래와 같다.
num[3][7] <= num[3][8] <= num[4][8]
3부터 7까지의 최소합비용의 인덱스 <= 3부터 8까지의 최소합비용의 인덱스 <= 4부터 8까지의 최소합비용의 인덱스
즉, 위에 있는 1~10 까지의 그림에서 ①,②,③ 이 위에서 말한 최소합 비용을 구하는 인덱스이다.
정확한 증명은 너무 복잡하여 제대로 판단하기 어렵지만, 통상적으로는 ①,②,③이 차이가 매우 미비하여(k에 비해)
거의 무시할만한 수치이고 이는 알고리즘에 그대로 반영되어
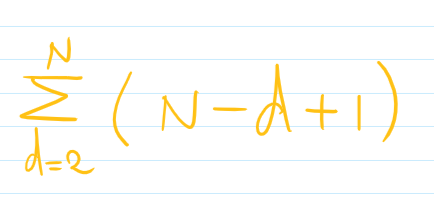
위의 식처럼 나오게 되고 O(N2)이 된다.
>> 소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | int main() { for (scanf("%d", &T); T--;) { scanf("%d", &N); for (int i = 1; i <= N; i++) scanf("%d", &novel[i]), psum[i] = psum[i - 1] + novel[i]; for (int i = 1; i <= N; i++) num[i - 1][i] = i; for (int d = 2; d <= N; d++) { for (int i = 0; i + d <= N; i++) { int j = i + d; dp2[i][j] = 2e9; for (int k = num[i][j - 1]; k <= num[i + 1][j]; k++) { int v = dp2[i][k] + dp2[k][j] + psum[j] - psum[i]; if (dp2[i][j] > v) dp2[i][j] = v, num[i][j] = k; } } } printf("%d\n", dp2[0][N]); } return 0; } | cs |
아직도 실력이 너무 딸린다.
연습이 많이 필요한 것 같다.
프로그래밍을 보면서 쳐보지 않고, 개념적인 부분만 익혔는데 다시 풀어봐야겠다.