[백준] 12738번 C/C++ 풀이 _ 가장 긴 증가하는 수열 3

- 출처 : https://www.acmicpc.net/problem/12738

시간 제한	메모리 제한	제출	정답	맞은 사람	정답 비율
3 초	512 MB	1161	609	497	58.956%

문제

수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.

예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.

입력

첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다.

둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (-1,000,000,000 ≤ Ai ≤ 1,000,000,000)

출력

첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.

예제 입력 1

6
10 20 10 30 20 50

예제 출력 1

출처

문제를 만든 사람: baekjoon
데이터를 추가한 사람: harinboy

비슷한 문제

- 풀이

풀이가 처음에 떠오르지 않아서 결국 다른 분의 도움을 받게 되었습니다.

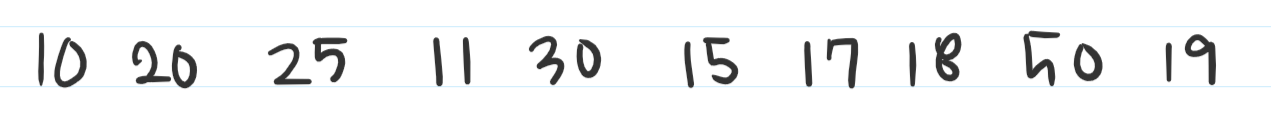
위와 같은 수열이 있다고 가정해보겠습니다.
위의 수열에서 가장 긴 증가하는 수열은 아래와 같습니다.

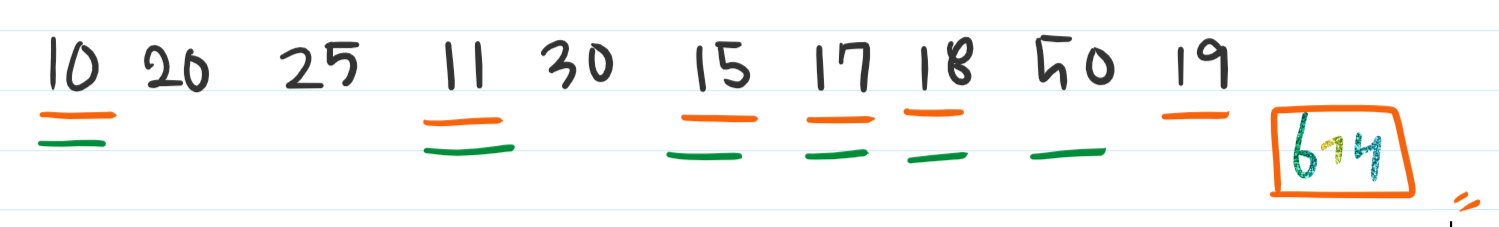
풀이 방법은 아래의 과정을 따라가면 됩니다.
먼저, 최장 증가 수열에 대한 길이를 알기 위한 배열이 하나 필요합니다.

해당 배열에는 특징이 있습니다.
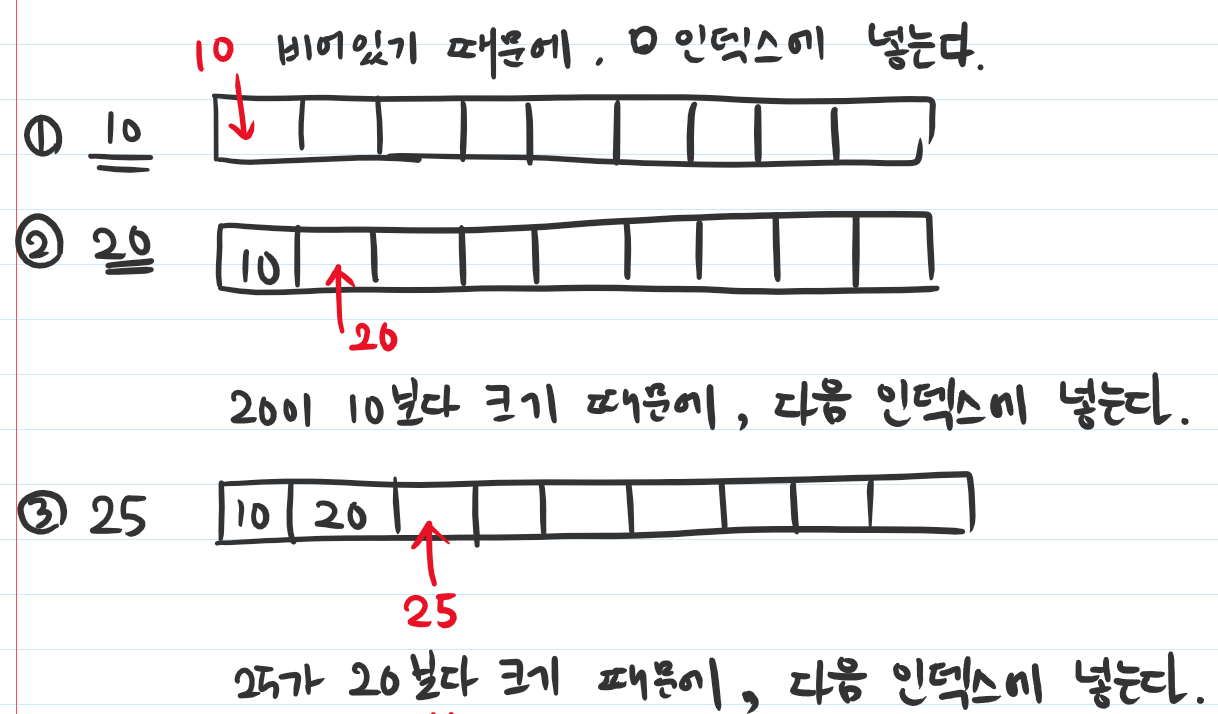
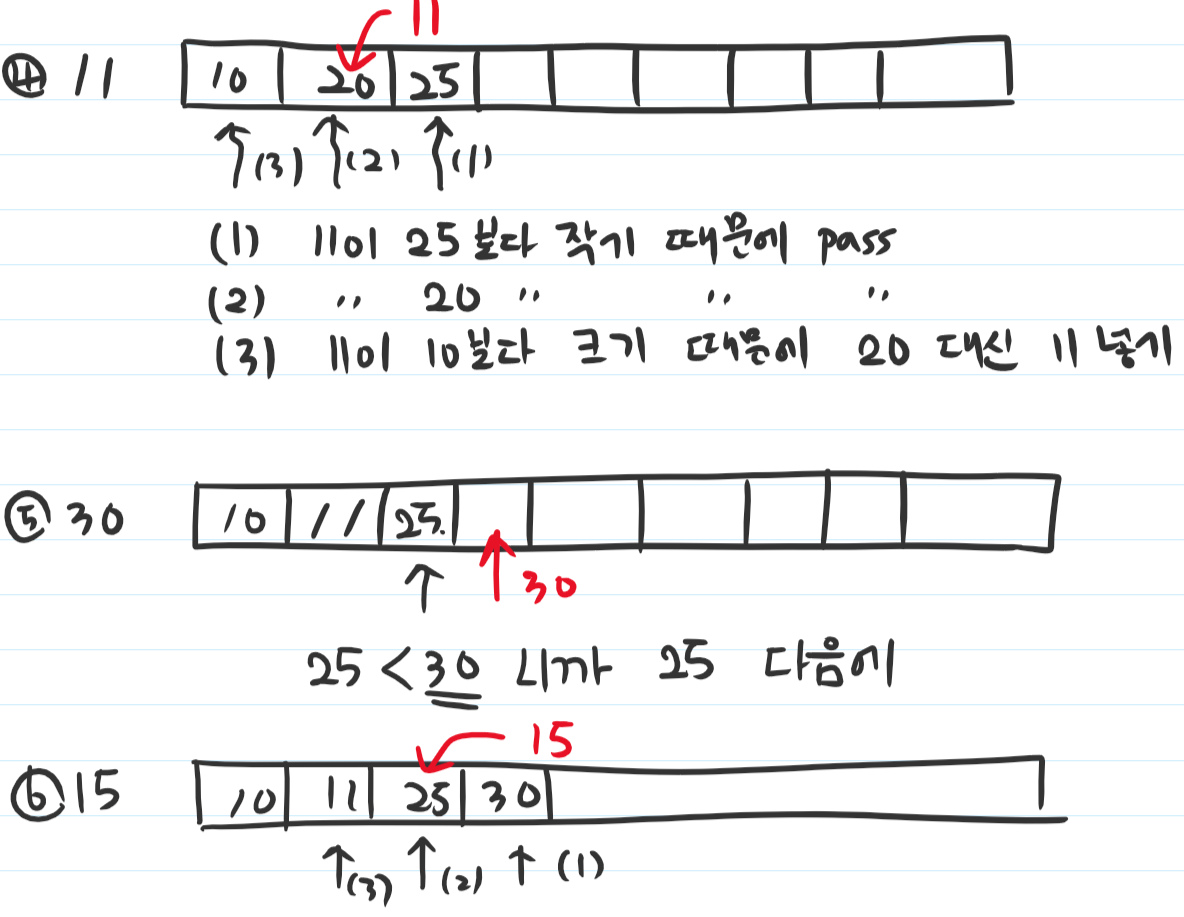
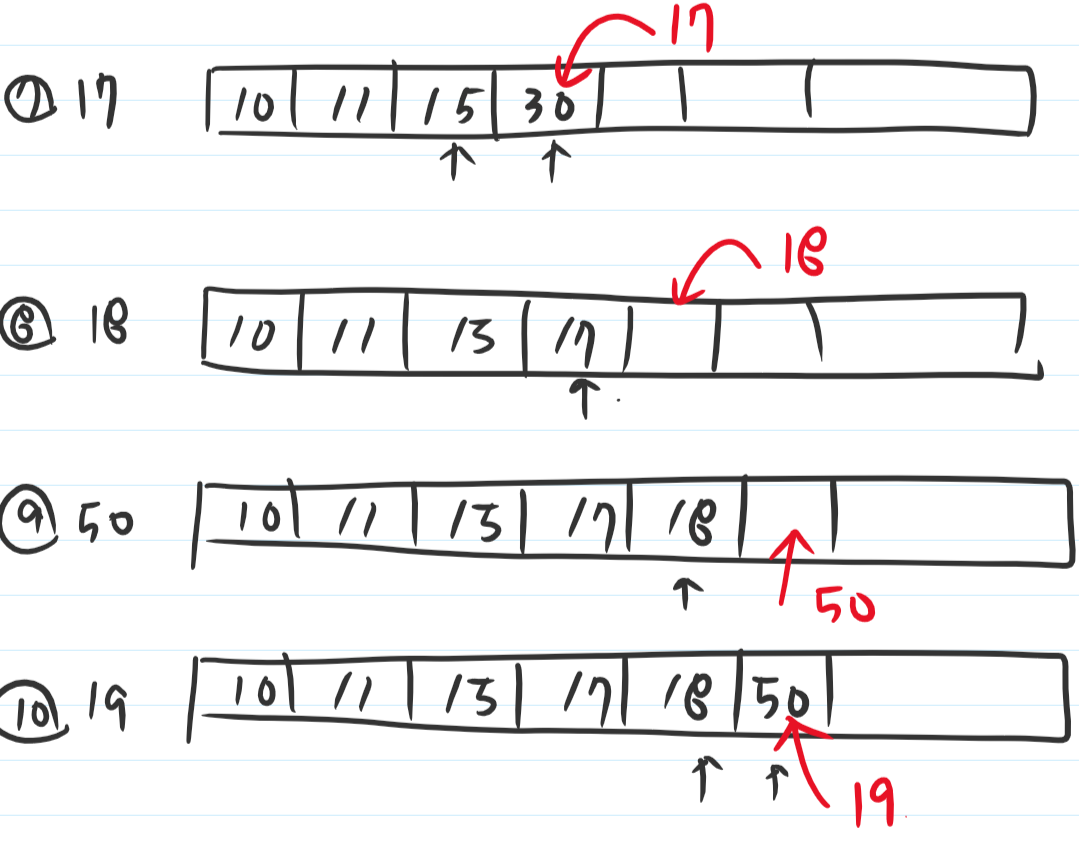
- 값이 있는 부분의 뒤에서 부터 탐색합니다.
- 탐색 인덱스의 값보다 새로 들어올 값이 클 경우에는, 탐색 인덱스 다음 자리에 넣어줍니다.
- 탐색 인덱스가 맨 처음 인덱스까지 가도 자신보다 작은 인덱스를 못 찾으면, 맨 처음에 넣어 줍니다.
- 항상 배열에 들어간 숫자의 개수가 최장 수열의 길이입니다.

아래는 위의 예시를 수행하는 과정을 그림으로 표시해 본 것입니다.

- 소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <vector>
#include <algorithm>
 
using namespace std;
 
///////////////////////////////////
////////// 전역 변수 ///////////////
///////////////////////////////////
int N; 
vector<int> answer_vec;
 
///////////////////////////////////
////////// 메인 함수 ///////////////
///////////////////////////////////
int main() {
    cin >> N;
 
    // 초기값 받기 
    int sub; 
    cin >> sub; 
    answer_vec.push_back(sub);
 
    // 벡터에 값 대입받기 
    for (int n_idx = 1; n_idx < N; n_idx++) {
        int sub; 
        cin >> sub; 
 
        // 크기 확인.    뒤에서 부터 접근하면서 크기를 확인한다. 
        int ans_vec_size = answer_vec.size();
        for (int conf_idx = ans_vec_size-1; conf_idx >=0 ; conf_idx--) {
            // sub 가 더 크면 현재 인덱스의 다음 인덱스에 밀어 넣는다. 
            if (answer_vec.at(conf_idx) < sub ) {
                // 만약 마지막 인덱스보다 값이 크면 push 를 사용하여 추가하고, 
                // 아니면 값을 교체한다.  
                if (conf_idx == ans_vec_size - 1) answer_vec.push_back(sub);
                else answer_vec.at(conf_idx+ 1 ) = sub;
                break;
            } 
            // 맨 첫 번째 인덱스 까지 갔는데 교체가 없으면, 0번 인덱스와 교환
            if ( conf_idx == 0 ) answer_vec.at(0) = sub;
        }
 
    }
 
    cout << answer_vec.size();
 
    return 0;
}
Colored by Color Scripter
cs

하지만 !! 이 문제의 풀이를 쓰던 중에 복잡도를 계산해보니 위의 문제가 풀리면 안될 것 같습니다.

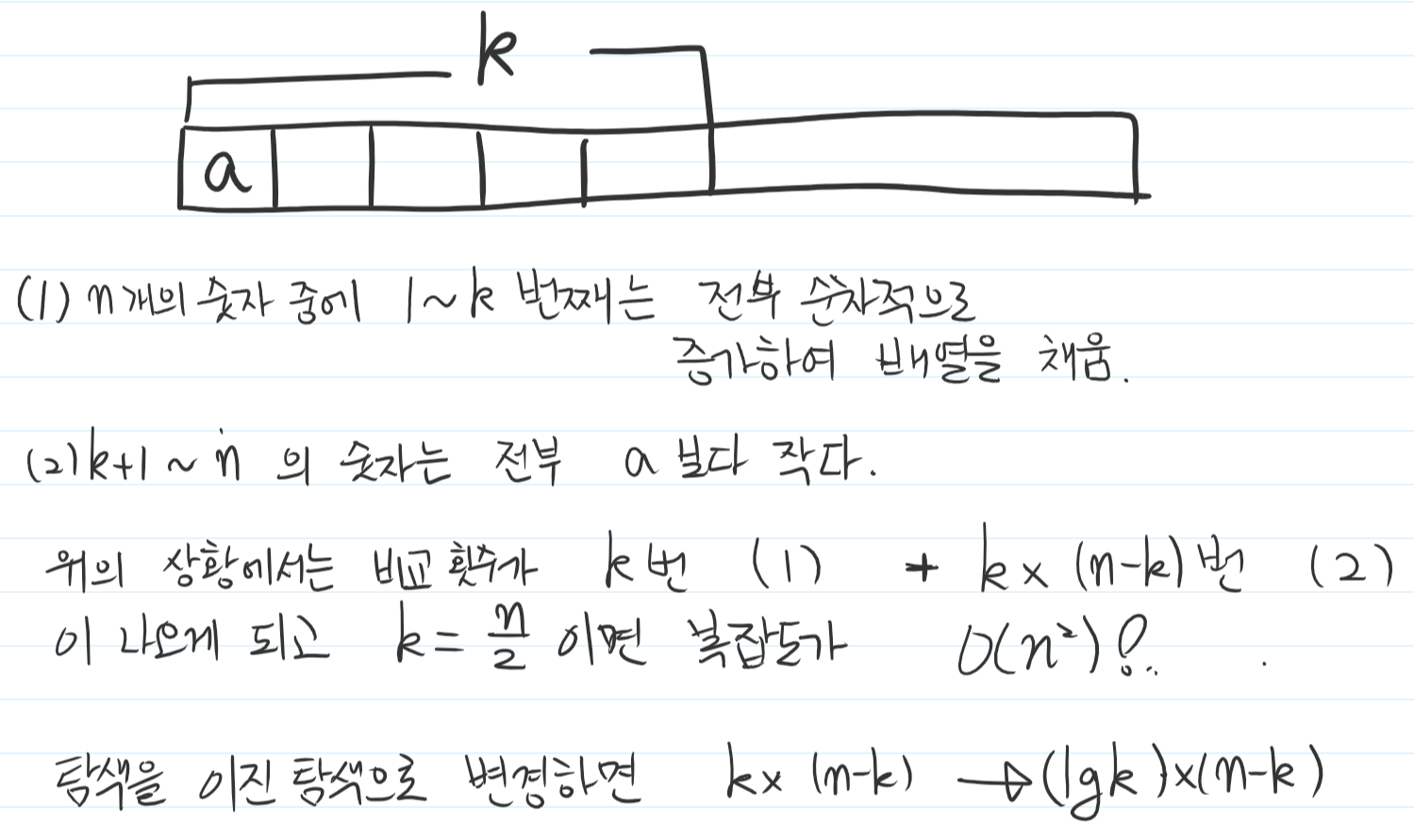
위와 같은 계산으로 인하여 '이진탐색' 이 필요합니다.

위 소스코드로도 통과했지만, 운이 좋아서 통과한 느낌입니다.

아래와 같이 lower_bound 함수를 사용해야합니다.(정렬된 곳에서만 사용 가능한 이분탐색 함수 )

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
#include<algorithm>
#include<vector>
#include<iterator>
using namespace std;
 
vector<int> vt;
vector<int>::iterator iter;
 
int main(void) {
    
    ios::sync_with_stdio(false);
    cin.tie(0);
 
    int n, data;
 
    cin >> n;
    for (int i = 0; i < n; i++) {
 
        cin >> data;
        if (i == 0) vt.push_back(data);
        if (vt.back() < data) vt.push_back(data);
        else {
            iter = lower_bound(vt.begin(), vt.end(), data);
            *iter = data;
        }
    }
 
    cout << vt.size();
 
    return 0;
}
Colored by Color Scripter
cs