- 출처 : https://www.acmicpc.net/problem/2133
타일 채우기 성공
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 128 MB | 11182 | 3880 | 3012 | 35.278% |
문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
예제 입력 1
2
예제 출력 1
3
힌트
아래 그림은 3×12 벽을 타일로 채운 예시이다.

출처
Contest > Waterloo's local Programming Contests > 24 September, 2005 D번
- 문제의 오타를 찾은 사람: imgosari
- 풀이 방법
아래와 같이 끝이 튀어나온 곳을 기준으로 0~11 가지의 케이스를 나눕니다.
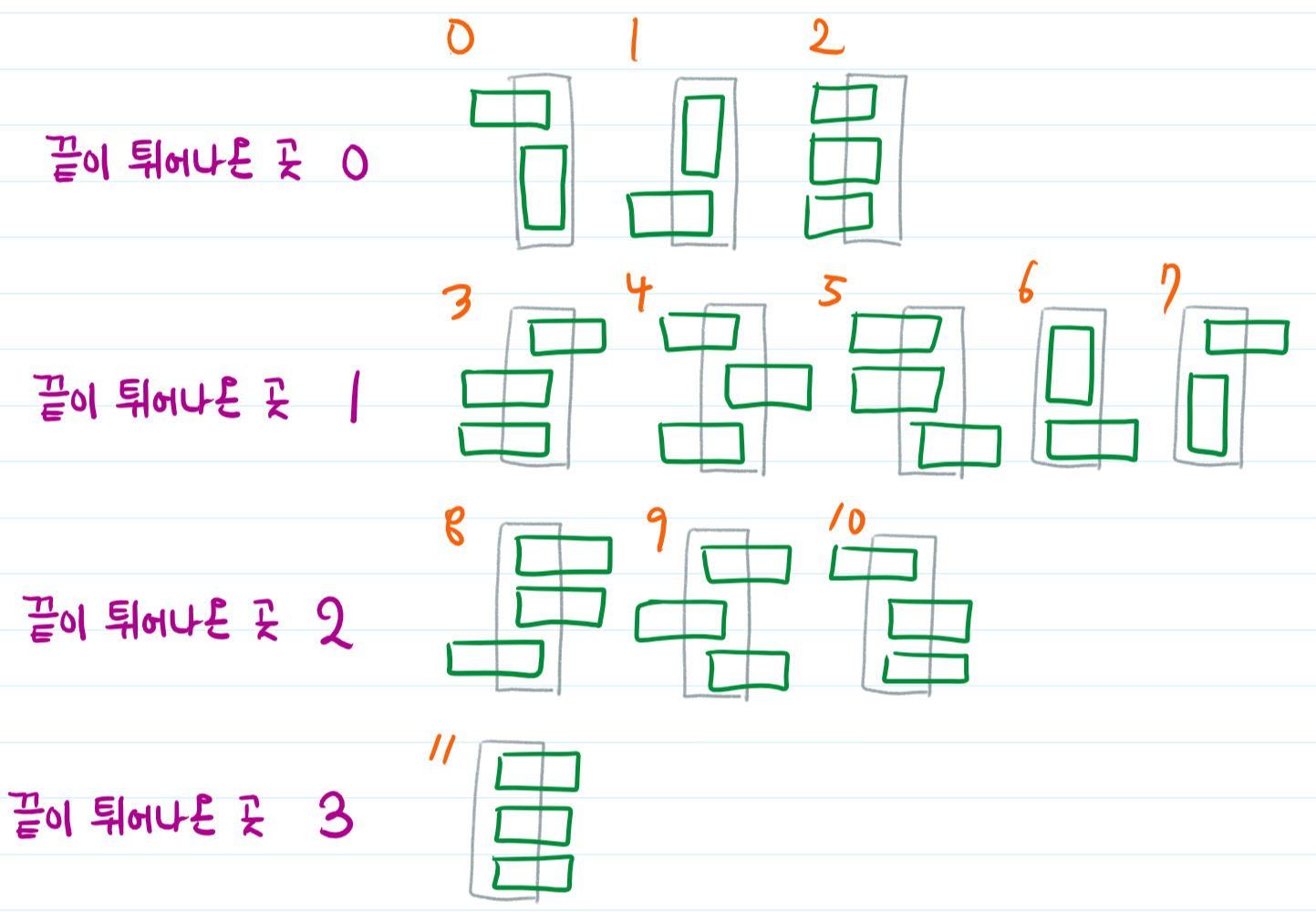
행의 위치를 한 번씩 증가시키면서, 12가지 케이스에 대해서 지속적으로 갱신합니다.
행의 위치를 갱신시켰다는 것은 해당 행을 모두 채웠다는 것을 의미합니다.
각각의 행을 갱신할 때, 이어진 이전 블록의 위치와 개수에 맞춰서 현재 블록을 갱신합니다.
예를 들어서, 4번째 행이 0번째 블록이 들어가면 맨 위의 블록이 이전 블록에서 끝이 튀어나왔습니다.
그러한 블록은 3번과 7번 상태가 있기 때문에, 3번째 행의 두 인덱스들을 더한 값이 4행의 0번째 블록이 들어갈 수 있는 개수입니다.
모든 과정을 수행한 수에, N번째 행렬의 값에서 끝이 튀어나오지 않은 것들을 모두 더해주면 정답입니다.
- 소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 | #include<iostream> #include<algorithm> #include<vector> using namespace std; #define SHAPE 12 #define MAX_ARR 30 + 1 int N; int dp[MAX_ARR][SHAPE]; int main(void) { // input cin >> N; // init dp[0][6] = dp[0][7] = dp[0][11] = 1; for (int dp_idx = 1; dp_idx < N; dp_idx++) { for (int shape_idx = 0; shape_idx < SHAPE; shape_idx++) { switch (shape_idx) { case 0: dp[dp_idx][shape_idx] = dp[dp_idx-1][3] + dp[dp_idx - 1][7]; break; case 1: dp[dp_idx][shape_idx] = dp[dp_idx - 1][5] + dp[dp_idx - 1][6]; break; case 2: dp[dp_idx][shape_idx] = dp[dp_idx - 1][11]; break; case 3: dp[dp_idx][shape_idx] = dp[dp_idx - 1][10]; break; case 4: dp[dp_idx][shape_idx] = dp[dp_idx - 1][9]; break; case 5: dp[dp_idx][shape_idx] = dp[dp_idx - 1][8]; break; case 6: dp[dp_idx][shape_idx] = dp[dp_idx - 1][0] + dp[dp_idx - 1][1] + dp[dp_idx - 1][2]; break; case 7: dp[dp_idx][shape_idx] = dp[dp_idx - 1][0] + dp[dp_idx - 1][1] + dp[dp_idx - 1][2]; break; case 8: dp[dp_idx][shape_idx] = dp[dp_idx - 1][5] + dp[dp_idx - 1][6]; break; case 9: dp[dp_idx][shape_idx] = dp[dp_idx - 1][4]; break; case 10: dp[dp_idx][shape_idx] = dp[dp_idx - 1][3] + dp[dp_idx - 1][7]; break; case 11: dp[dp_idx][shape_idx] = dp[dp_idx - 1][0] + dp[dp_idx - 1][1] + dp[dp_idx - 1][2]; break; default: printf("out of index!!"); break; } } } cout << dp[N - 1][0] + dp[N - 1][1] + dp[N - 1][2]; return 0; } | cs |