Easy is Perfect

[백준] 10973번 C/C++ 풀이 _ 이전 순열

  • melonicedlatte
  • Aug 05, 2018


출처 : https://www.acmicpc.net/problem/10973 



이전 순열 성공

시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율
1 초 256 MB 1978 1269 1099 66.525%

문제

1부터 N까지의 수로 이루어진 순열이 있다. 이 때, 사전순으로 바로 이전에 오는 순열을 구하는 프로그램을 작성하시오.

사전 순으로 가장 앞서는 순열은 오름차순으로 이루어진 순열이고, 가장 마지막에 오는 순열은 내림차순으로 이루어진 순열이다.

N = 3인 경우에 사전순으로 순열을 나열하면 다음과 같다.

  • 1, 2, 3
  • 1, 3, 2
  • 2, 1, 3
  • 2, 3, 1
  • 3, 1, 2
  • 3, 2, 1

입력

첫째 줄에 N(1 ≤ N ≤ 10,000)이 주어진다. 둘째 줄에 순열이 주어진다.

출력

첫째 줄에 입력으로 주어진 순열의 이전에 오는 순열을 출력한다. 만약, 사전순으로 가장 처음에 오는 순열인 경우에는 -1을 출력한다.

예제 입력 1 

4
1 2 3 4

예제 출력 1 

-1

예제 입력 2 

5
5 4 3 2 1

예제 출력 2 

5 4 3 1 2

출처

알고리즘 분류





























풀이

이번 문제의 풀이에는 '재귀함수'를 사용했다. (풀고 나니 끝에서 부터 찾으면 재귀함수 필요 없을 것 같다. )


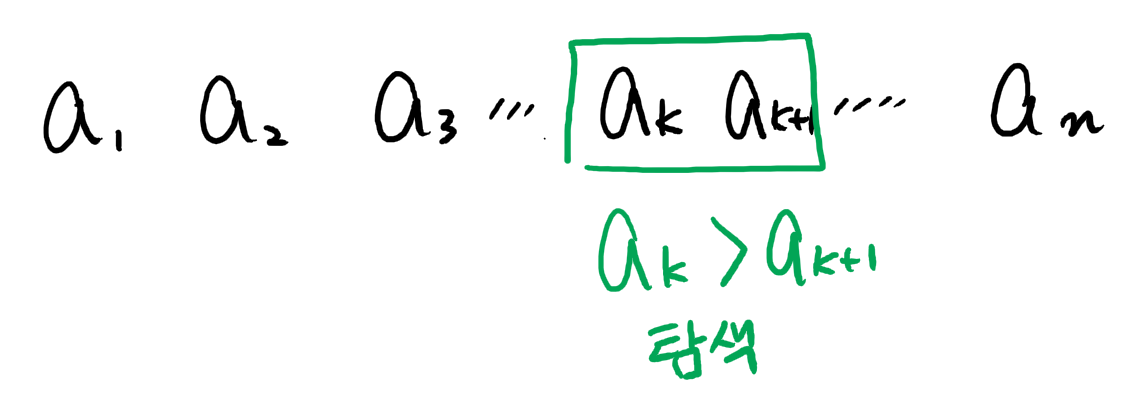
주어진 수열에서 숫자가 감소하는 부분을 탐색한다. 
해당 부분은 이전 수열이 될 때 '바뀔 수 있는 부분' 이다. 

해당 부분을 찾았다면 ak+1 부분부터 끝까지 탐색하여 다시 요소 중에 왼쪽 요소가 오른쪽 요소보다 더 큰 구간을 찾는다. 



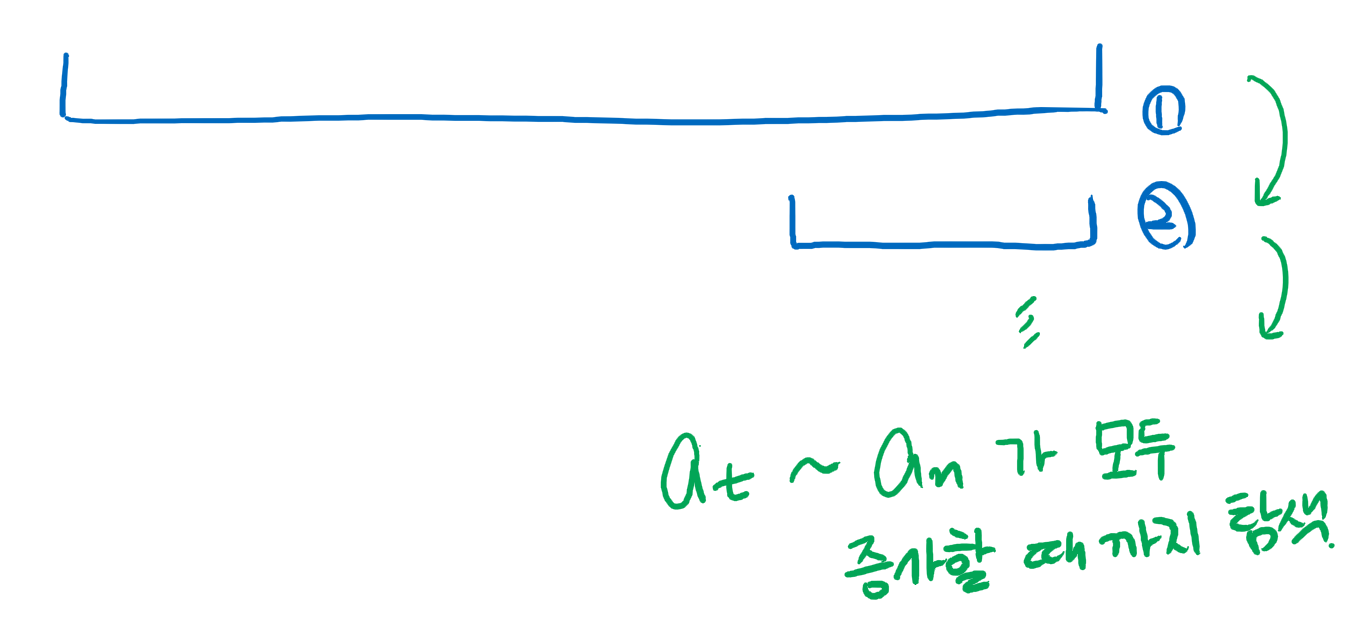
구간을 계속 내려가면서 전부 증가하는 구간을 찾는다. 
at~an  구간과 at-1 의 값을 변경하여 답을 찾아야 한다. 


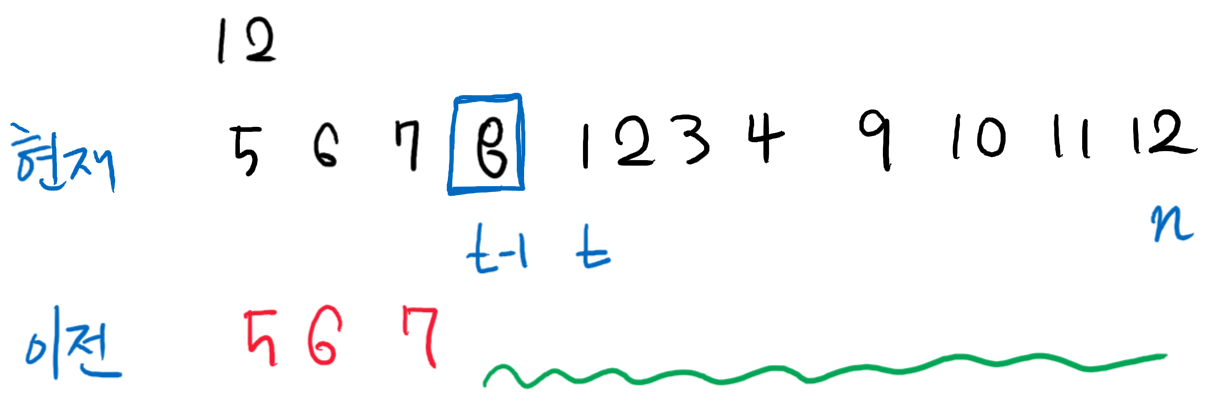
예를 들어, 현재의 수열이 위와 같다고 생각해보자. 
위에서 찾은 가장 우측의  at-1 > at  인 t 는 1이 위치한 인덱스이다. 

이 경우에 t-1 이전의 모든 인덱스 들은 값이 변하지 않는다. 
[t-1 , n] 사이의 값을 변경해주면 이전 수열을 구할 수 있다. 


변경하는 방법은 8 보다 적은 바로 이전의 수를 골라서 지금 8의 위치에 넣고, 나머지는 크기가 큰 순서대로 넣어주는 것이다. 
이 문제에서는 재귀로 구현하는 것이 for문으로 구현하는 것 보다 훨씬 어렵고 귀찮은 작업 같다. 



소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
#pragma warning(disable : 4996)
using namespace std;
 
int N;
vector<int> num_vec;
vector<int> answer_vec;
 
int is_find_before(int start, int end) {
    int sear_idx;
    for (sear_idx = start; sear_idx < end; sear_idx++) {
        if (num_vec.at(sear_idx) < num_vec.at(sear_idx + 1))
            answer_vec.at(sear_idx) = num_vec.at(sear_idx);
        else break;
    }
 
    if (sear_idx >= end) return 0;
 
    // we find descend sector
    int is_find_before_flag = is_find_before(sear_idx + 1, end);
 
    // there is no any descend sector
    if (is_find_before_flag == 0) {
        // 현재 인덱스 보다 한 칸 작은 놈을 선택 
        auto _iter = lower_bound(num_vec.begin() + sear_idx + 1 , num_vec.end(), num_vec.at(sear_idx));
        int one_small_index = _iter - num_vec.begin()-1;
        int one_small_value = num_vec.at(one_small_index);
        answer_vec.at(sear_idx) = num_vec.at(one_small_index);
 
        // 한 칸 작은 놈을 현재 위치에 넣어주고 나머지는 반대로 정렬해서 하나씩 넣어준다. 
        sort(num_vec.begin() + sear_idx + 1, num_vec.end(), greater<int>() );
 
        for (int new_idx = sear_idx + 1; new_idx <= end; new_idx++)
            if (one_small_value == num_vec.at(new_idx))
                answer_vec.at(new_idx) = num_vec.at(sear_idx);
            else
                answer_vec.at(new_idx) = num_vec.at(new_idx);
    }
 
    return 1;
}
 
int main() {
 
    scanf("%d", &N);
    num_vec.resize(N, 0);
    answer_vec.resize(N, 0);
 
    for (int n_idx = 0; n_idx < N; n_idx++)
        scanf("%d", &num_vec.at(n_idx));
 
    int is_get_answer = is_find_before(0, N - 1);
 
    if (!is_get_answer) {
        printf("-1");
        return 0;
    }
 
    for (int n_idx = 0; n_idx < N; n_idx++)
        printf("%d ", answer_vec.at(n_idx) ? answer_vec.at(n_idx) : num_vec.at(n_idx));
 
    return 0;
}
cs


아래는 stl 을 사용한 간단한 풀이이다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<cstdio>
#include<algorithm>
using namespace std;
#define MAX 10000
 
int s[MAX];
 
int main()
{
 
    int n;
    scanf("%d", &n);
 
    for (int i = 0; i < n; ++i)
        scanf("%d", &s[i]);
 
    if (prev_permutation(&s[0], &s[n]))
        for (int i = 0; i < n; ++i)
            printf("%d ", s[i]);
    else 
        printf("-1");
 
}
cs



Search