출처 : https://www.acmicpc.net/problem/1865
웜홀 성공
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 128 MB | 4197 | 1423 | 913 | 31.581% |
문제
때는 2020년, 백준이는 월드나라의 한 국민이다. 월드 나라에는 N개의 지점이 있고 N개의 지점 사이에는 M개의 도로와 W개의 웜홀이 있다. (단 도로는 방향이 없으며 웜홀은 방향이 있다.) 웜홀은 시작 위치에서 도착 위치로 가는 하나의 경로인데, 특이하게도 도착을 하게 되면 시작을 하였을 때 보다 시간이 뒤로 가게 된다. 웜홀 내에서는 시계가 거꾸로 간다고 생각하여도 좋다.
시간 여행을 매우 좋아하는 백준이는 한 가지 궁금점에 빠졌다. 1번 지점에서 출발을 하여서 시간여행을 하기 시작하여 다시 출발을 하였던 위치로 돌아왔을 때, 출발을 하였을 때 보다 시간이 되돌아 가 있는 경우가 있는지 없는지 궁금해졌다. 여러분은 백준이를 도와 이런 일이 가능한지 불가능한지 구하는 프로그램을 작성하여라.
입력
첫번째 줄에는 테스트케이스의 개수 T(1≤T≤5)가 주어진다. 그리고 두 번째 줄부터 T개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫번째 줄에는 지점의 수 N(1≤N≤500), 도로의 개수 M(1≤M≤2500), 웜홀의 개수(1≤W≤200)이 주어진다. 그리고 두번째 줄부터 M+1개의 줄까지 도로의 정보가 주어지는데 각 도로의 정보는 S,E,T 세 정수로 주어진다. S와 E는 연결된 지점의 번호, T는 이 도로를 통해 이동하는데 걸리는 시간을 의미한다. 그리고 M+2~M+W+1번째 줄까지 웜홀의 정보가 S,E,T 세 정수로 주어지는데 S는 시작 지점, E는 도착 지점, T는 줄어드는 시간을 의미한다. T는 10,000보다 작거나 같은 자연수 또는 0이다.
두 지점을 연결하는 도로가 한 개보다 많을 수도 있다.
출력
T개의 줄에 걸쳐서 만약에 시간이 줄어들면서 출발 위치로 돌아오는 것이 가능하면 YES, 불가능하면 NO를 출력한다.
예제 입력 1
2 3 3 1 1 2 2 1 3 4 2 3 1 3 1 3 3 2 1 1 2 3 2 3 4 3 1 8
예제 출력 1
NO YES
출처
Olympiad > USA Computing Olympiad > 2006-2007 Season > USACO December 2006 Contest > Gold 1번
- 문제의 오타를 찾은 사람: adgdsda
- 빠진 조건을 찾은 사람: joeyvalentine kipa00 progresivojs wooljs
풀이
이 문제는 벨만-포드 알고리즘으로 해결합니다.
벨만-포드 알고리즘의 설명은 아래의 링크를 따라가면 자세히 볼 수 있습니다.
http://algo-revolution.blogspot.kr/2016/05/bellman-ford-algorithm.html
http://www.crocus.co.kr/534
https://ratsgo.github.io/data%20structure&algorithm/2017/11/27/bellmanford/
https://www.acmicpc.net/board/view/21965 (백준 알고리즘 아이디 필요)
벨만 포드 알고리즘을 이용하여 음의 간선을 찾아냅니다.
이 문제에서 약간 헤맸던 것은 "음의 가중치가 있으면 출발 노드인 1번 노드가 벨만 포드 알고리즘을 수행하면 음수값이 되어있을 것이다." 라는 가정 때문입니다.
해당 반례를 찾아내었습니다.
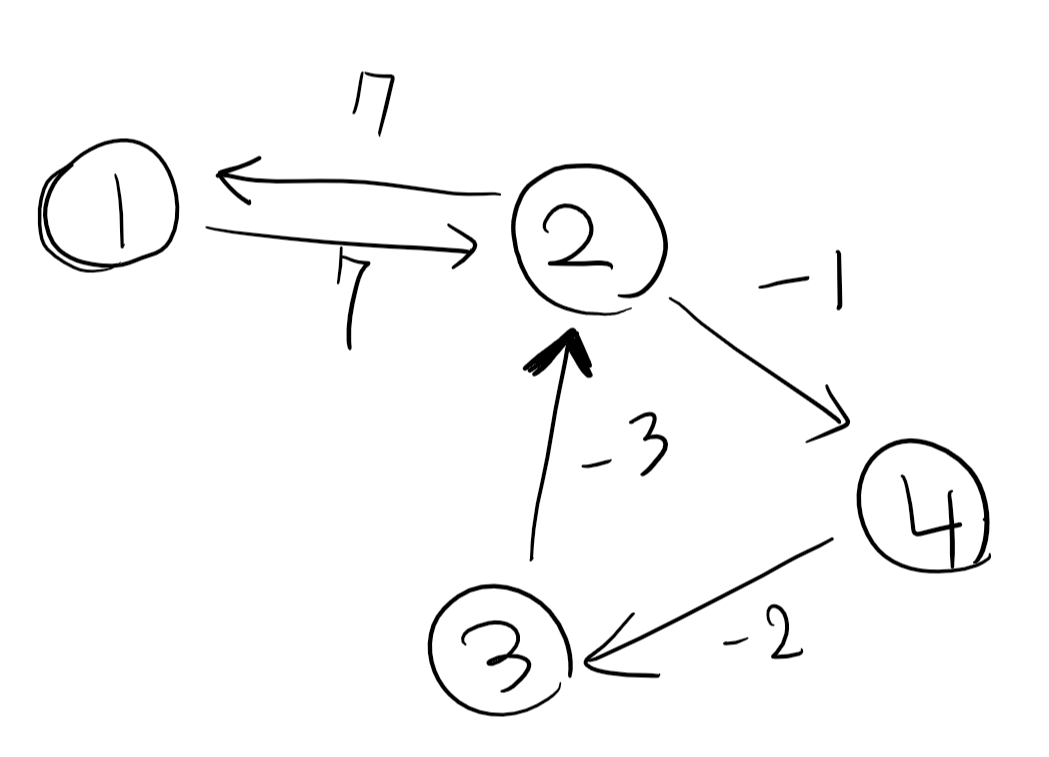
위와 같은 구조를 이루고 있으면 N번을 갱신 하더라도 dis[1]이 음수가 되지 않습니다.
그 이유는 2번 노드의 가중치가 -7 보다 작아야 1이 갱신되는데, 음의 사이클이 존재하더라도 N번의 수행으로 답이 나오지 않을 수 있다.
N 번째에 갱신이 되었는지 안되었는지를 체크해주어서 음의 사이클만 확인하면 답이 나온다.
소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | #include <iostream> #include <vector> using namespace std; #define N_MAX 500 + 1 #define INF 987654321 #define START 1 int main() { int T, N, M, W; cin >> T; while (T--) { cin >> N >> M >> W; // pair 의 앞은 목적지, 뒤는 가중치 vector<vector<pair<int,int>>> edge(N + 1); vector<int> dis(N + 1, INF); dis.at(START) = 0; // M 갱신 for (int m_idx = 0; m_idx < M; m_idx++) { int node_1_, node_2_, weight_; cin >> node_1_ >> node_2_ >> weight_; edge.at(node_1_).push_back({ node_2_ , weight_ }); edge.at(node_2_).push_back({ node_1_ , weight_ }); } // W 갱신 for (int w_idx = 0; w_idx < W; w_idx++) { int from_, to_, weight_; cin >> from_ >> to_ >> weight_; edge.at(from_).push_back({ to_ , (-1)*weight_ }); } // 모든 엣지들에 대하여 갱신한다. int is_have_cycle = 0; for (int t_idx = 1; t_idx <= N; t_idx++){ for (int v_idx = 1; v_idx <= N; v_idx++){ int edge_size_ = edge.at(v_idx).size(); for (int e_idx = 0; e_idx < edge_size_; e_idx++) { int from_ = v_idx; int to_ = edge.at(v_idx).at(e_idx).first; int weight_ = edge.at(v_idx).at(e_idx).second; if ( dis.at(from_) + weight_ < dis.at(to_)) { dis.at(to_) = dis.at(from_) + weight_; if (t_idx==N) is_have_cycle = 1; } } } } is_have_cycle ? printf("YES\n") : printf("NO\n"); } return 0; } | cs |