Easy is Perfect

[백준] 1309번 C/C++ 풀이 _ 동물원

  • melonicedlatte
  • Aug 25, 2018


출처 : https://www.acmicpc.net/problem/1309

동물원 성공

시간 제한메모리 제한제출정답맞은 사람정답 비율
2 초128 MB58732973242049.651%

문제

어떤 동물원에 가로로 두칸 세로로 N칸인 아래와 같은 우리가 있다.

이 동물원에는 사자들이 살고 있는데 사자들을 우리에 가둘 때, 가로로도 세로로도 붙어 있게 배치할 수는 없다. 이 동물원 조련사는 사자들의 배치 문제 때문에 골머리를 앓고 있다.

동물원 조련사의 머리가 아프지 않도록 우리가 2*N 배열에 사자를 배치하는 경우의 수가 몇 가지인지를 알아내는 프로그램을 작성해 주도록 하자. 사자를 한 마리도 배치하지 않는 경우도 하나의 경우의 수로 친다고 가정한다.

입력

첫째 줄에 우리의 크기 N(1≤N≤100,000)이 주어진다.

출력

첫째 줄에 사자를 배치하는 경우의 수를 9901로 나눈 나머지를 출력하여라.

예제 입력 1 

4

예제 출력 1 

41

출처

  • 문제의 오타를 찾은 사람: joon8409
  • 문제를 만든 사람: xhark

알고리즘 분류

문제풀이


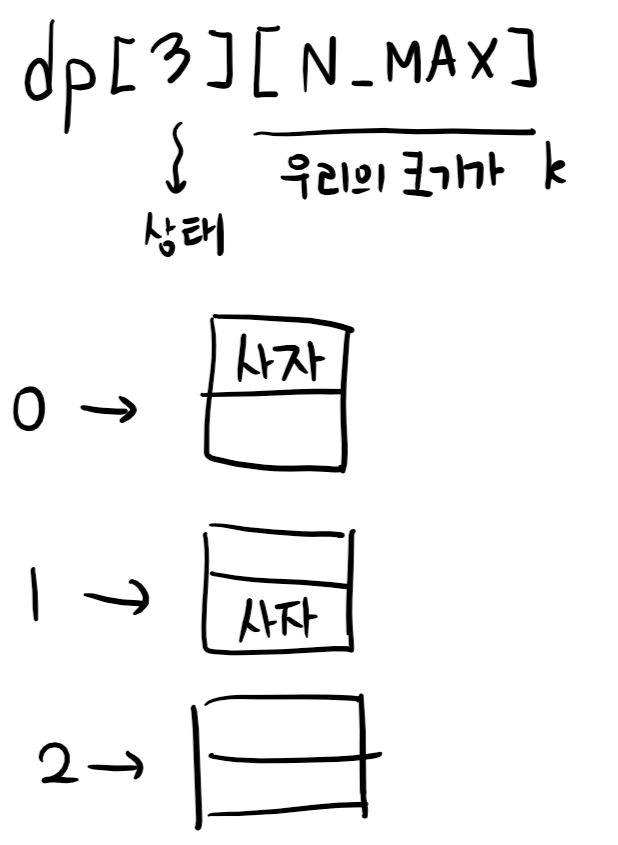
dp[i][k]가 의미하는 바는 i 의 상태에서 k의 높이일 때 가능한 경우의 수입니다. 

// 0번 인덱스의 상태 

// 0 -> 이전 위에 칸에 사자가 있었다

// 1 -> 이전 아래 칸에 사자가 있었다

// 2 -> 이전 칸에는 사자가 없었다 

위의 구조를 가진 dp 배열을 생성합니다. 



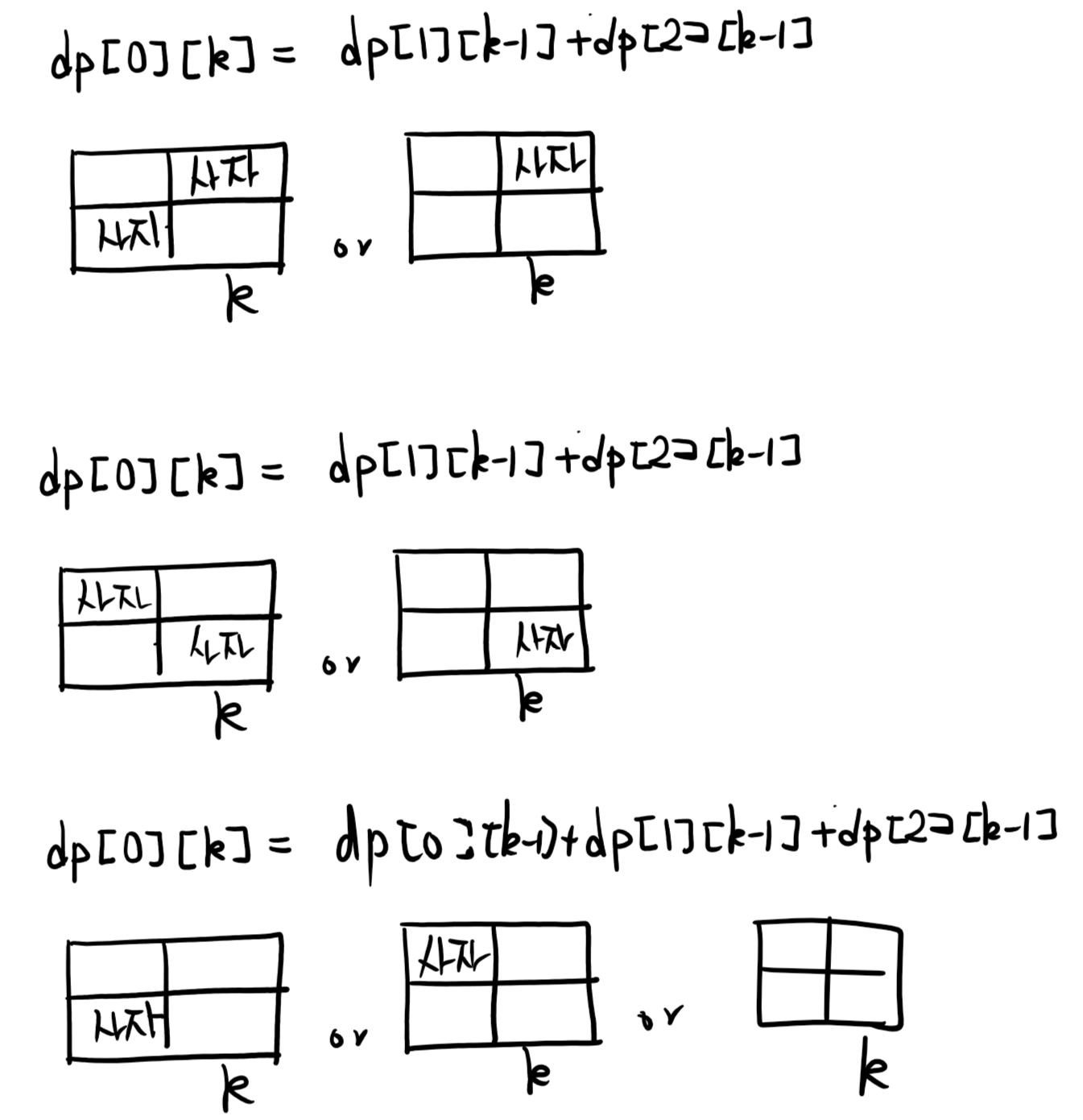
위와 같이 이전 상태를 살펴보고 k 의 상태 값을 갱신할 수 있습니다. 

갱신할 때마다 % 9901 을 해줘야 overflow 가 나지 않는다. (int, long long) 에서 모두 다 에러가 발생 합니다.

자세한 구현은 소스코드를 참조하세요~

소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <algorithm>
using namespace std;
#define N_MAX 100000 + 1 
#define DIV 9901
 
int main() {
    ios::sync_with_stdio(false);
 
    int N;
    // 0번 인덱스의 상태 
    // 0 -> 이전 위에 칸에 사자가 있었다
    // 1 -> 이전 아래 칸에 사자가 있었다
    // 2 -> 이전 칸에는 사자가 없었다 
    int cage_dp[3][N_MAX] = { 0 };
    cin >> N;
 
    cage_dp[0][1] = 1;
    cage_dp[1][1] = 1;
    cage_dp[2][1] = 1;
 
    for (int n_idx = 2; n_idx <= N; n_idx++) {
        cage_dp[0][n_idx] = (cage_dp[1][n_idx - 1] + cage_dp[2][n_idx - 1])%DIV;
        cage_dp[1][n_idx] = (cage_dp[0][n_idx - 1] + cage_dp[2][n_idx - 1])%DIV;
        cage_dp[2][n_idx] = (cage_dp[0][n_idx - 1] + cage_dp[1][n_idx - 1] + cage_dp[2][n_idx - 1])%DIV;
    }
 
    cout << (cage_dp[0][N] + cage_dp[1][N] + cage_dp[2][N]) % DIV;
 
    return 0;
}
cs



Search