출처 : https://www.acmicpc.net/problem/6603
로또 성공
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 128 MB | 7291 | 4020 | 2889 | 55.239% |
문제
독일 로또는 {1, 2, ..., 49}에서 수 6개를 고른다.
로또 번호를 선택하는데 사용되는 가장 유명한 전략은 49가지 수 중 k(k>6)개의 수를 골라 집합 S를 만든 다음 그 수만 가지고 번호를 선택하는 것이다.
예를 들어, k=8, S={1,2,3,5,8,13,21,34}인 경우 이 집합 S에서 수를 고를 수 있는 경우의 수는 총 28가지이다. ([1,2,3,5,8,13], [1,2,3,5,8,21], [1,2,3,5,8,34], [1,2,3,5,13,21], ..., [3,5,8,13,21,34])
집합 S와 k가 주어졌을 때, 수를 고르는 모든 방법을 구하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있다. 첫 번째 수는 k (6 < k < 13)이고, 다음 k개 수는 집합 S에 포함되는 수이다. S의 원소는 오름차순으로 주어진다.
입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스마다 수를 고르는 모든 방법을 출력한다. 이 때, 사전 순으로 출력한다.
각 테스트 케이스 사이에는 빈 줄을 하나 출력한다.
예제 입력 1
7 1 2 3 4 5 6 7 8 1 2 3 5 8 13 21 34 0
예제 출력 1
1 2 3 4 5 6 1 2 3 4 5 7 1 2 3 4 6 7 1 2 3 5 6 7 1 2 4 5 6 7 1 3 4 5 6 7 2 3 4 5 6 7 1 2 3 5 8 13 1 2 3 5 8 21 1 2 3 5 8 34 1 2 3 5 13 21 1 2 3 5 13 34 1 2 3 5 21 34 1 2 3 8 13 21 1 2 3 8 13 34 1 2 3 8 21 34 1 2 3 13 21 34 1 2 5 8 13 21 1 2 5 8 13 34 1 2 5 8 21 34 1 2 5 13 21 34 1 2 8 13 21 34 1 3 5 8 13 21 1 3 5 8 13 34 1 3 5 8 21 34 1 3 5 13 21 34 1 3 8 13 21 34 1 5 8 13 21 34 2 3 5 8 13 21 2 3 5 8 13 34 2 3 5 8 21 34 2 3 5 13 21 34 2 3 8 13 21 34 2 5 8 13 21 34 3 5 8 13 21 34
풀이
가능한 로또의 경우의 수를 모두 출력하는 문제입니다.
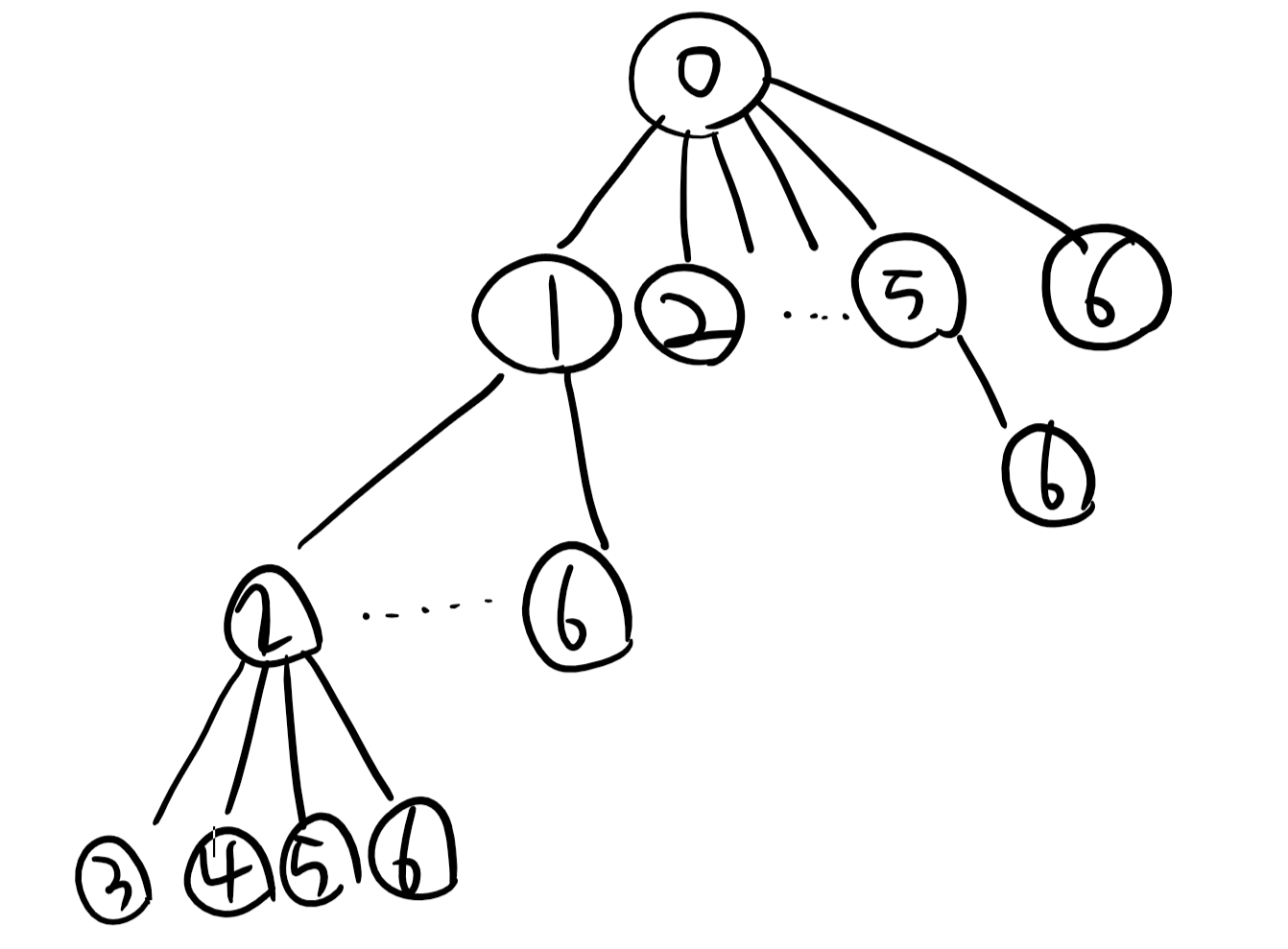
0~6 의 인덱스를 가진 숫자(7개의 숫자)가 있다고 가정해보면 위와 같은 트리를 그릴 수 있습니다.
루트 노드에 대하여 자식 노드들은 루트 노드보다 항상 큰 값을 가지는 트리를 구성하게 됩니다.
위와 같이 서브트리에서의 루트 자식들은 항상 루트보다 작은 값을 가진 상태로 dfs 를 사용해서 갱신합니다.
그리고 높이가 6이 되는 순간 가능한 원소들을 출력해주고 더 이상 탐색을 하지 않으면 문제가 해결됩니다.
저는 재귀함수를 이용하여 dfs 를 구현했습니다.
one_answer 라는 벡터를 사용해서 dfs 가 시작할 때, 새로운 숫자를 넣어주고 끝날 때에는 pop_back 을 이용하여 빼주었습니다.
이번에는 일부로 전역변수를 사용하지 않고 프로그래밍을 진행하여 파라미터가 조금 많습니다.
더 간결하게 풀기 위해서는 전역변수를 쓰면 보기 더 깔끔합니다
http://jun-itworld.tistory.com/15
위의 링크를 참조하면 조금 더 간결한 풀이를 확인하실 수 있습니다.
소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 | #include <iostream> #include <vector> #define SIZE 6 using namespace std; void dfs(int _n, vector<int>& _num_vec, vector<int>& _one_answer, int _now_idx) { int answer_size = _one_answer.size(); // 사이즈가 원하는사이즈 보다 크면 종료 if (answer_size > SIZE) return; // 출력하고 끝내기 if (answer_size == SIZE) { for (int ans_idx = 0; ans_idx < SIZE; ans_idx++) cout << _num_vec[_one_answer[ans_idx]] << " "; cout << "\n"; return; } // 다음 단계 dfs 가능한 노드들을 _one_answer에 추가해주는 구간 for (int n_idx = _now_idx + 1; n_idx < _n; n_idx++) { // 만약, 6개를 채울 수 없는 위치의 인덱스를 선택하면 종료 if (answer_size + (_n - n_idx) < SIZE) return; _one_answer.push_back(n_idx); dfs(_n, _num_vec, _one_answer, n_idx); _one_answer.pop_back(); } } int main() { ios::sync_with_stdio(false); while (1) { int n; cin >> n; if (n == 0) break; // input vector<int> num_vec(n, 0); vector<int> one_answer; for (int n_idx = 0; n_idx < n; n_idx++) cin >> num_vec.at(n_idx); // dfs 수행 for (int n_idx = 0; n_idx < n; n_idx++) { one_answer.push_back(n_idx); dfs(n, num_vec, one_answer, n_idx); one_answer.pop_back(); } cout << "\n"; } return 0; } | cs |