Easy is Perfect

[백준] 2056번 C/C++ 풀이 _ 작업

  • melonicedlatte
  • Aug 31, 2018


출처 : https://www.acmicpc.net/problem/2056 

작업 성공

시간 제한메모리 제한제출정답맞은 사람정답 비율
2 초128 MB232092666637.970%

문제

수행해야 할 작업 N개 (3 ≤ N ≤ 10000)가 있다. 각각의 작업마다 걸리는 시간(1 ≤ 시간 ≤ 100)이 정수로 주어진다.

몇몇 작업들 사이에는 선행 관계라는 게 있어서, 어떤 작업을 수행하기 위해 반드시 먼저 완료되어야 할 작업들이 있다. 이 작업들은 번호가 아주 예쁘게 매겨져 있어서, K번 작업에 대해 선행 관계에 있는(즉, K번 작업을 시작하기 전에 반드시 먼저 완료되어야 하는) 작업들의 번호는 모두 1 이상 (K-1) 이하이다. 작업들 중에는, 그것에 대해 선행 관계에 있는 작업이 하나도 없는 작업이 반드시 하나 이상 존재한다. (1번 작업이 항상 그러하다)

모든 작업을 완료하기 위해 필요한 최소 시간을 구하여라. 물론, 서로 선행 관계가 없는 작업들은 동시에 수행 가능하다.

입력

첫째 줄에 N이 주어진다.

두번째 줄부터 N+1번째 줄까지 N개의 줄이 주어진다. 2번째 줄은 1번 작업, 3번째 줄은 2번 작업, ..., N+1번째 줄은 N번 작업을 각각 나타낸다. 각 줄의 처음에는, 해당 작업에 걸리는 시간이 먼저 주어지고, 그 다음에 그 작업에 대해 선행 관계에 있는 작업들의 개수(0 ≤ 개수 ≤ 100)가 주어진다. 그리고 선행 관계에 있는 작업들의 번호가 주어진다.

출력

첫째 줄에 모든 작업을 완료하기 위한 최소 시간을 출력한다.

예제 입력 1 

7
5 0
1 1 1
3 1 2
6 1 1
1 2 2 4
8 2 2 4
4 3 3 5 6

예제 출력 1 

23

힌트

  •  1번 작업 : 0~5  2번 작업 : 5~6
  •  3번 작업 : 6~9  4번 작업 : 5~11
  •  5번 작업 : 11~12 6번 작업 : 11~19
  •  7번 작업 : 19~23

출처

풀이


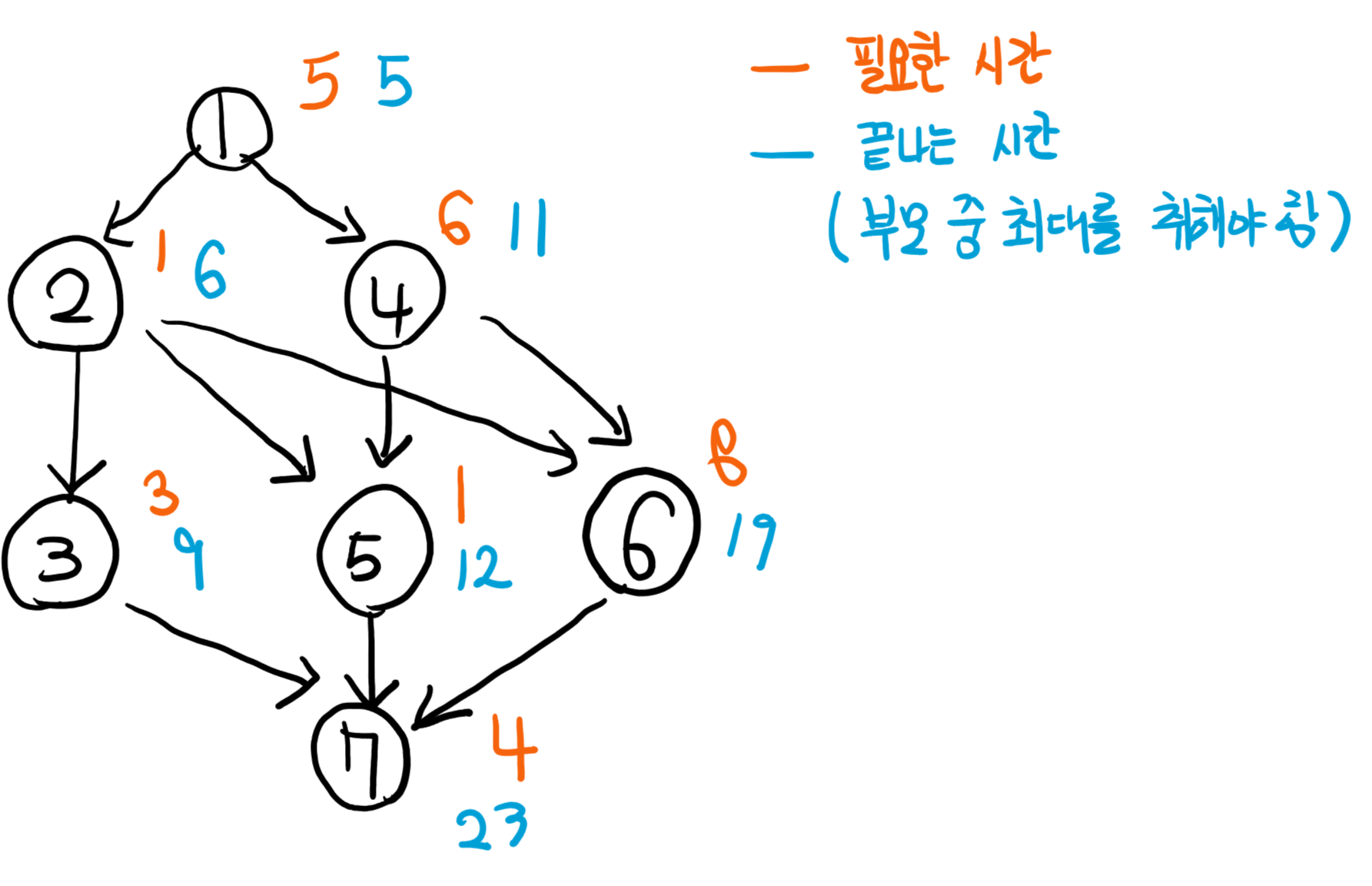
예제에 나오는 문제를 위와 같이 표기해 보았습니다. 
각 노드에서 필요한 시간을 주황색으로 표시하고, 끝나는 시간을 부모 중 최대 + 현재 노드의 필요한 시간으로 취해야 합니다. 

부모노드를 저장하는 벡터를 선언한 다음, 해당 벡터를 탐색하면서 답을 도출합니다. 
자세한 구현은 소스코드를 참조해주세요~

소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream> 
#include <vector>
#include <algorithm>
using namespace std;
 
int main(void) {
    ios::sync_with_stdio(false);
    int N;
    cin >> N;
 
    vector<int> finish_time(N + 1);
    vector<int> spend_time(N + 1);
    vector<vector<int>> parent_node(N + 1);
    // input
    for (int n_idx = 1; n_idx <= N; n_idx++) {
        int K;
        cin >> spend_time[n_idx] >> K;
        while (K--) {
            int sub_parent;
            cin >> sub_parent;
            parent_node[n_idx].push_back(sub_parent);
        }
    }
    // 부모 노드의 값을 보고 각각을 갱신 
    for (int n_idx = 1; n_idx <= N; n_idx++) {
        int parent_size = parent_node[n_idx].size();
        int parent_time_max = 0;
        for (int par_idx = 0; par_idx < parent_size; par_idx++)
            if(parent_time_max < finish_time[parent_node[n_idx][par_idx]])
                parent_time_max = finish_time[parent_node[n_idx][par_idx]]; 
 
        finish_time[n_idx] = parent_time_max + spend_time[n_idx];
    } 
    // 최대값 취하기
    int max_time = 0 ; 
    for (int n_idx = 1; n_idx <= N; n_idx++)
        if (max_time < finish_time[n_idx])
            max_time = finish_time[n_idx];
 
    cout << max_time;
    return 0;
}
cs



Search