Easy is Perfect

[백준] 11051번 C/C++ 풀이 _ 이항 계수 2

  • melonicedlatte
  • Sep 26, 2018


출처 : https://www.acmicpc.net/problem/11051 

이항 계수 2

시간 제한메모리 제한제출정답맞은 사람정답 비율
1 초256 MB105183911311138.379%

문제

자연수 N과 정수 K가 주어졌을 때 이항 계수 (NK)를 10,007로 나눈 나머지를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ K ≤ N)

출력

 (NK)를 10,007로 나눈 나머지를 출력한다.

예제 입력 1 

5 2

예제 출력 1 

10

출처

알고리즘 분류


풀이 

위와 같은 형태의 식으로 이항 계수를 구할 수 있습니다. (출처 : 위키백과) 
하지만 곱으로 구하면 수가 너무 커서 int 형이나 long long 형태의 오버플로우가 일어납니다. 

이와 같은 경우에서는 dp 를 이용하여 풀면 쉽게 풀 수 있습니다. 


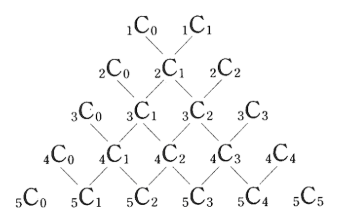
이항 계수는 위와 같은 형태로 규칙을 이용하여 구할 수 있습니다. 
이미지 출처 : https://samtoring.com/qstn/QST0026495.png 

위와 같은 항등식을 이용하여 구할 수 있습니다. (출처 : 위키백과)

자세한 풀이는 소스코드를 참조해주세요~

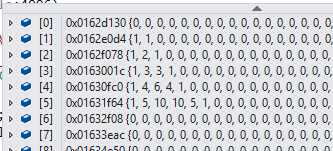
+ 5와 2를 입력하여 dp 배열을 살펴보면 위와 같은 모습을 가지고 있는 것을 확인할 수 있습니다. 

소스코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
using namespace std; 
#define DIV_NUM 10007
#define NK_MAX 1000 + 1 
int main() {
    int N, K; scanf("%d %d", &N, &K);
    int dp[NK_MAX][NK_MAX] = { 0 };
    // for 문을 이용하여 n이 1일때부터 갱신합니다.
    // 각 라운드에서는 k가 0~n 가지일 때를 갱신합니다.
    for(int n_row = 1; n_row <= N; n_row++){
        for (int k_col = 0; k_col <= N; k_col++) {
            if (n_row == k_col || k_col == 0) {
                dp[n_row][k_col] = 1; continue;
            }
            dp[n_row][k_col] = (dp[n_row - 1][k_col] + dp[n_row - 1][k_col - 1]) % DIV_NUM;
        }
    }
    printf("%d", dp[N][K]);
    return 0;
}
cs



Search