출처 : https://www.acmicpc.net/problem/15685
드래곤 커브 성공
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 512 MB | 2197 | 1114 | 779 | 49.776% |
문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- 시작 점
- 시작 방향
- 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.

즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점이 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
- 0: x좌표가 증가하는 방향 (→)
- 1: y좌표가 감소하는 방향 (↑)
- 2: x좌표가 감소하는 방향 (←)
- 3: y좌표가 증가하는 방향 (↓)
출력
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
예제 입력 1
3 3 3 0 1 4 2 1 3 4 2 2 1
예제 출력 1
4
예제 입력 2
4 3 3 0 1 4 2 1 3 4 2 2 1 2 7 3 4
예제 출력 2
11
예제 입력 3
10 5 5 0 0 5 6 0 0 5 7 0 0 5 8 0 0 5 9 0 0 6 5 0 0 6 6 0 0 6 7 0 0 6 8 0 0 6 9 0 0
예제 출력 3
8
예제 입력 4
4 50 50 0 10 50 50 1 10 50 50 2 10 50 50 3 10
예제 출력 4
1992
힌트
 |  |
| 예제 1 | 예제 2 |
출처
- 문제를 만든 사람: baekjoon
풀이
이 문제는 삼성 기출 문제입니다.
기존의 문제와 약간 다른 컨셉으로 시뮬레이션 문제를 출제한 것 같습니다.
구현 방법은 다음과 같습니다.
각각의 드래곤 커브에 대한 입력을 받고, 벡터에 드래곤 커브들의 좌표를 하나하나씩 넣습니다.
그리고 1세대의 드래곤 커브가 생성되면 아래와 같이 회전 변환 개념을 사용했습니다. 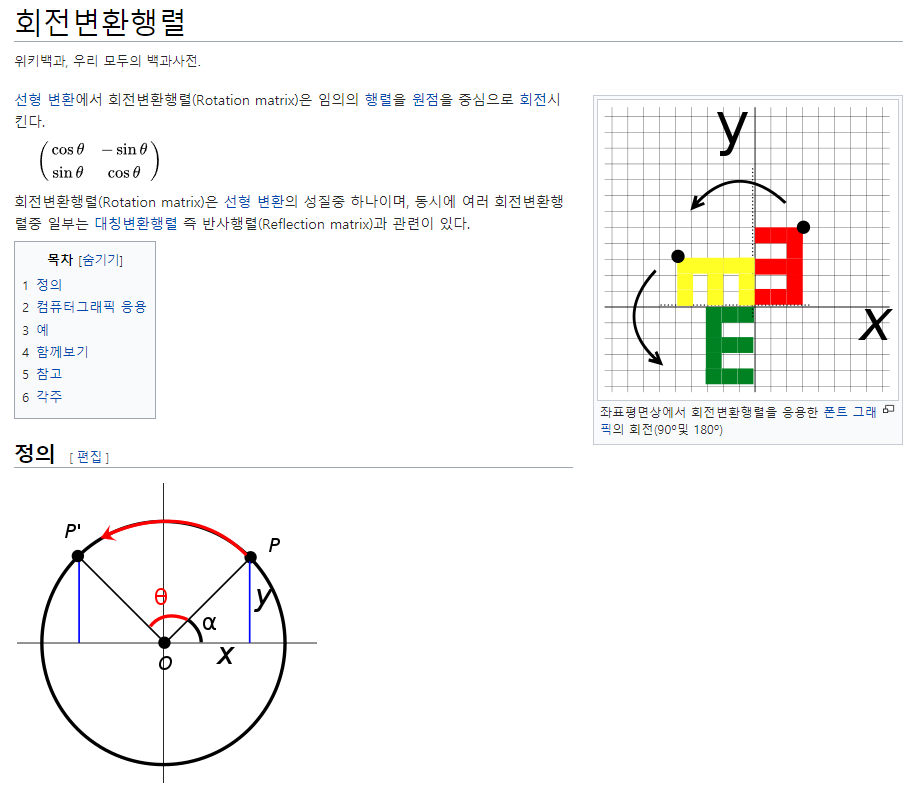
https://ko.wikipedia.org/wiki/%ED%9A%8C%EC%A0%84%EB%B3%80%ED%99%98%ED%96%89%EB%A0%AC
자세한 설명과 출처는 위키백과를 참조했습니다.
사실 이 문제에서 회전변환을 쓰지 않아도 되지만, 저는 그냥 그게 그 순간 떠올라서 그렇게 풀었습니다.
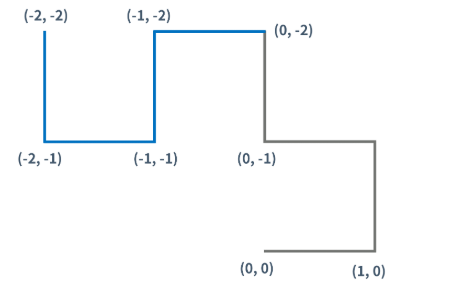
위의 드래곤 커브를 보면, 기존 세대의 마지막 점을 기준으로 시계 방향으로 90도를 회전변환을 하기 때문에,
해당 지식을 이용해서 소스코드를 구현했습니다.
마지막 점을 pivot으로 생각하고, 그 이전의 점들을 모두 pivot을 기준으로 회전변환을 해주었습니다.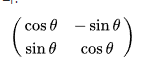
이 때, pivot 을 원점으로 생각하고 평행이동을 해주고 나서, 위와 같은 공식을 사용하여 회전하고,
다시 원래 위치로 평행이동을 했습니다.
그리고 마지막에 방문한 노드를 확인해서 정답을 출력했습니다.
자세한 풀이는 소스코드를 참조해주세요~
소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | #include <iostream> #include <vector> using namespace std; #define RC_MX 100 + 2 // global #pragma warning(disable:4996) #define SIDE 4 int side_arr[SIDE][2] = { { 1,0 },{ 0,-1 },{ -1,0 },{ 0,1 } }; // 드래곤 커브를 만드는 메소드 void make_dragon_curve(vector<pair<int, int>>& _dragon_curve, int _gene) { int make_num = _gene; while (make_num--) { int dragon_size = _dragon_curve.size(); // 가장 마지막 점이 회전의 기준 pair<int, int> pivot = _dragon_curve.back(); for (int dra_idx = dragon_size - 2; dra_idx >= 0; dra_idx--) { // 원점이동 -> 회전이동 -> 다시 이동 후에 삽입한다. pair<int, int> new_pivot = { _dragon_curve[dra_idx].first - pivot.first, _dragon_curve[dra_idx].second - pivot.second }; _dragon_curve.push_back({ -new_pivot.second + pivot.first, new_pivot.first + pivot.second }); } } } int main() { int is_visited[RC_MX][RC_MX] = { 0 }; int N; scanf("%d", &N); for (int n_idx = 0; n_idx < N; n_idx++) { int x, y, d, g; scanf("%d %d %d %d", &x, &y, &d, &g); // 드래곤 커브를 만든다. 벡터로 표현한다 vector<pair<int, int>> dragon_curve; dragon_curve.push_back({ x,y }); dragon_curve.push_back({ x + side_arr[d][0], y + side_arr[d][1] }); make_dragon_curve(dragon_curve, g); // 드래곤 커브가 도달할 수 있는 배열에 전부 표시한다. for (auto dot : dragon_curve) is_visited[dot.second][dot.first] = 1; } int answer = 0; for (int x_idx = 0; x_idx < RC_MX; x_idx++) for (int y_idx = 0; y_idx < RC_MX; y_idx++) // 4 사이드 전부 도달한 곳이면 ++ if (is_visited[x_idx][y_idx] && is_visited[x_idx][y_idx + 1] && is_visited[x_idx + 1][y_idx] && is_visited[x_idx + 1][y_idx + 1]) answer++; printf("%d", answer); return 0; } | cs |