엔트로피는 머신러닝을 할 때, loss function(손실 함수) or cost function으로써 많이 사용됩니다. 용어에 대하여는 많이 들어보았지만 직관적으로 다가오지가 않아서 한 번 정리해보았습니다.
1. Entropy
\[H(x)=−\sum_{i=1}^{n} p(x_i) log{p(x_i)}\]엔트로피는
불확실성의 척도입니다. 정보이론에서의 엔트로피는불확실성을 나타내며, 엔트로피가 높다는 것은 정보가 많고, 확률이 낮다는 것을 의미합니다.
이런 설명과 수식으로는 처음에는 와닿지가 않습니다. 제가 이해한 불확실성이라는 것은 어떤 데이터가 나올지 예측하기 어려운 경우라고 받아들이는 것이 더 직관적입니다. 예시를 통해 보는 것이 가장 좋습니다.
1.1. 예시 _ 동전 던지기 & 주사위 던지기
- 동전을 던졌을 때, 앞/뒷면이 나올 확률을 모두 1/2라고 하겠습니다.
- 주사위를 던졌을 때, 각 6면이 나올 확률을 모두 1/6이라고 하겠습니다.
위의 두 상황에서 불확실성(어떤 데이터가 나올지 예측하기 어려운 것)은 주사위가 더 크다고 직관적으로 다가옵니다. 이를 수식적으로 계산하면 각각 아래와 같습니다.
- $ H(x)= -\left( \frac{1}{2} log{\frac{1}{2}} + \frac{1}{2} log{\frac{1}{2}} \right) $
- $ H(x)= - \left( \frac{1}{6} log{\frac{1}{6}} + \frac{1}{6} log{\frac{1}{6}} + \frac{1}{6} log{\frac{1}{6}} + \frac{1}{6} log{\frac{1}{6}} + \frac{1}{6} log{\frac{1}{6}} + \frac{1}{6} log{\frac{1}{6}} \right) $
동전의 엔트로피 값은 약 0.693, 주사위의 엔트로피 값은 1.79 정도로 주사위의 엔트로피 값이 더 높다는 것을 알 수 있습니다. 즉, 무엇이 나올지 알기 어려운 주사위의 경우가 엔트로피가 더 높은 것이죠.
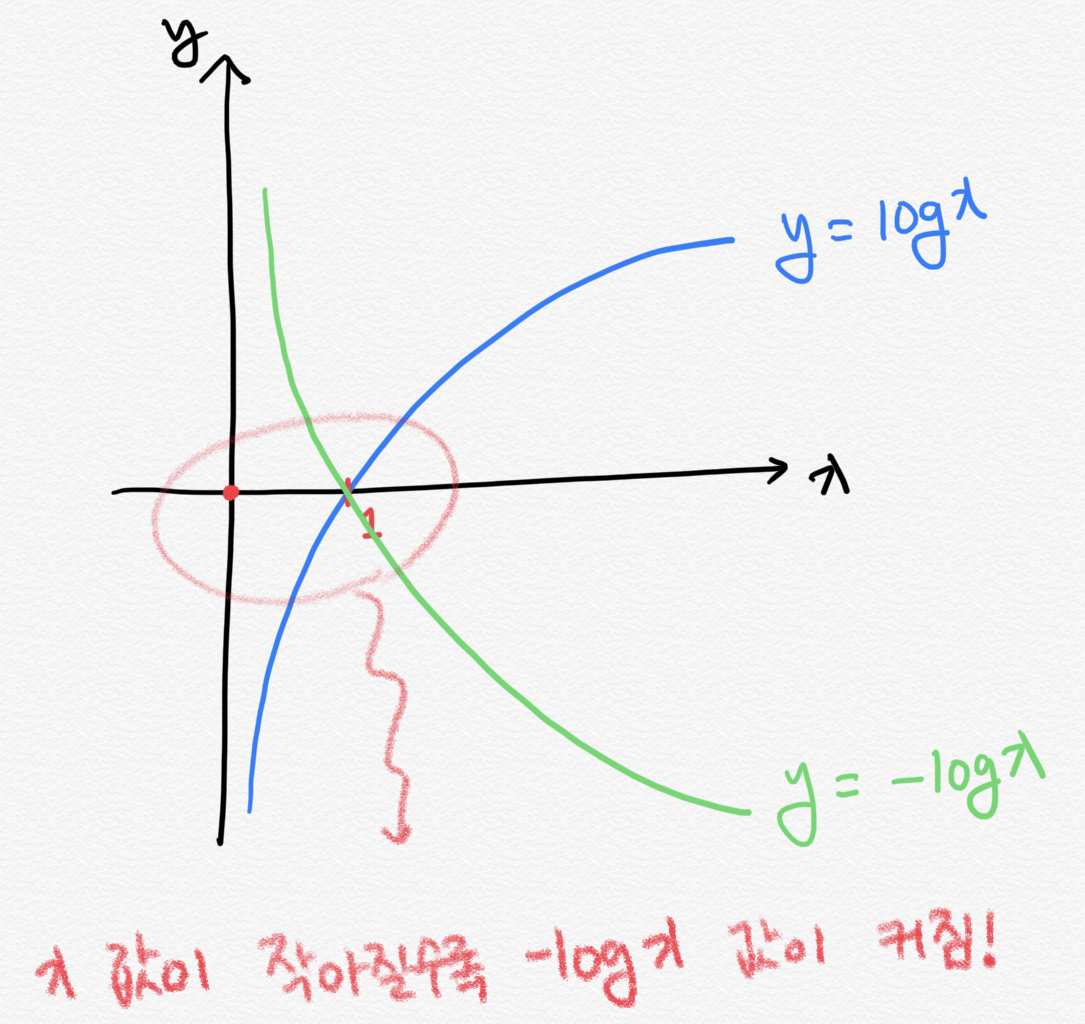
이를 위의 그래프를 통해 살펴보면 이렇게 해석할 수 있습니다.
\[H(x)=−\sum_{i=1}^{n} p(x_i) log{p(x_i)}\]위의 수식을 아래의 수식으로 바꿔봅니다.
\[H(x)=\sum_{i=1}^{n} p(x_i) \left( -log{p(x_i)} \right)\]$ p(x_i) $은 각각의 요소들이 나올 수 있는 확률값입니다. 모든 요소들이 나올 확률이 동일하다면, $ -log{p(x_i)} $ 값도 모두 동일하기 때문에 식을 간결하게 만들 수 있습니다.
$ p(x_i) $ 값의 총 합은 1이기 때문에, 그러므로 수식은 $ H(x)=\sum_{i=1}^{n} p(x_i) \left( -log{p(x_i)} \right) = -log{p(x_i)} $이 됩니다. $ x $ 값이 작아질수록 -logx 값이 기하급수적으로 커집니다. $x$가 작아진 것 보다 $log{x}$가 커지는 폭이 훨씬 크기 때문에, 전체 엔트로피는 증가하는 것입니다.
1.2. 공 꺼내기
다른 예시를 통해서 이해를 좀 더 돕겠습니다.
- 전체 공이 100개이다. 공 하나만 빨간색이고, 나머지는 모두 검은색이다.
- 전체 공이 100개이다. 공 50개는 빨간색이고, 나머지는 모두 검은색이다.
위의 경우에는 직관적으로 첫 번째 사례에서 검은 색이 나올 확률이 높으니 불확실성이 적겠군 이라고 생각할 수 있습니다. 실제로 엔트로피를 계산하면 후자가 훨씬 크게 나옵니다.
2. Cross-Entropy
\[H_p (q)=−\sum_{i=1}^{n} q(x_i) log{p(x_i)}\]크로스 엔트로피는 실제 분포 $ q $에 대하여 알지 못하는 상태에서, 모델링을 통하여 구한 분포인 $ p $를 통하여 $ q $ 를 예측하는 것입니다. $ q $와 $ p $가 모두 들어가서 크로스 엔트로피라고 한다고 합니다.
머신러닝을 하는 경우에 실제 환경의 값과 $ q $를, 예측값(관찰값) $ p $를 모두 알고 있는 경우가 있습니다. 머신러닝의 모델은 몇%의 확률로 예측했는데, 실제 확률은 몇%야!라는 사실을 알고 있을 때 사용합니다.
크로스 엔트로피에서는 실제값과 예측값이 맞는 경우에는 0으로 수렴하고, 값이 틀릴경우에는 값이 커지기 때문에, 실제 값과 예측 값의 차이를 줄이기 위한 엔트로피라고 보시면 될 것 같습니다.
출처
- https://3months.tistory.com/436
- https://m.blog.naver.com/PostView.nhn?blogId=roboholic84&logNo=221629115916&proxyReferer=https%3A%2F%2Flm.facebook.com%2F
- https://m.blog.naver.com/PostView.nhn?blogId=yonggeol93&logNo=221230536533&proxyReferer=https%3A%2F%2Fwww.google.co.kr%2F