출처 : https://www.acmicpc.net/problem/2240
자두나무 성공
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 128 MB | 4335 | 1859 | 1273 | 41.506% |
문제
자두는 자두를 좋아한다. 그래서 집에 자두나무를 심어두고, 여기서 열리는 자두를 먹고는 한다. 하지만 자두는 키가 작아서 자두를 따먹지는 못하고, 자두가 떨어질 때까지 기다린 다음에 떨어지는 자두를 받아서 먹고는 한다. 자두를 잡을 때에는 자두가 허공에 있을 때 잡아야 하는데, 이는 자두가 말랑말랑하여 바닥에 떨어지면 못 먹을 정도로 뭉개지기 때문이다.
매 초마다, 두 개의 나무 중 하나의 나무에서 열매가 떨어지게 된다. 만약 열매가 떨어지는 순간, 자두가 그 나무의 아래에 서 있으면 자두는 그 열매를 받아먹을 수 있다. 두 개의 나무는 그다지 멀리 떨어져 있지 않기 때문에, 자두는 하나의 나무 아래에 서 있다가 다른 나무 아래로 빠르게(1초보다 훨씬 짧은 시간에) 움직일 수 있다. 하지만 자두는 체력이 그다지 좋지 못해서 많이 움직일 수는 없다.
자두는 T(1≤T≤1,000)초 동안 떨어지게 된다. 자두는 최대 W(1≤W≤30)번만 움직이고 싶어 한다. 매 초마다 어느 나무에서 자두가 떨어질지에 대한 정보가 주어졌을 때, 자두가 받을 수 있는 자두의 개수를 구해내는 프로그램을 작성하시오. 자두는 1번 자두나무 아래에 위치해 있다고 한다.
입력
첫째 줄에 두 정수 T, W가 주어진다. 다음 T개의 줄에는 각 순간에 자두가 떨어지는 나무의 번호가 1 또는 2로 주어진다.
출력
첫째 줄에 자두가 받을 수 있는 자두의 최대 개수를 출력한다.
예제 입력 1
7 2 2 1 1 2 2 1 1
예제 출력 1
6
풀이
다이나믹 프로그래밍을 이용해야 풀리는 문제입니다.
트리를 이용하여 dfs 같은 구조를 사용하면 최대 이동 회수가 2^1000 이기 때문에 너무 큰 숫자입니다.
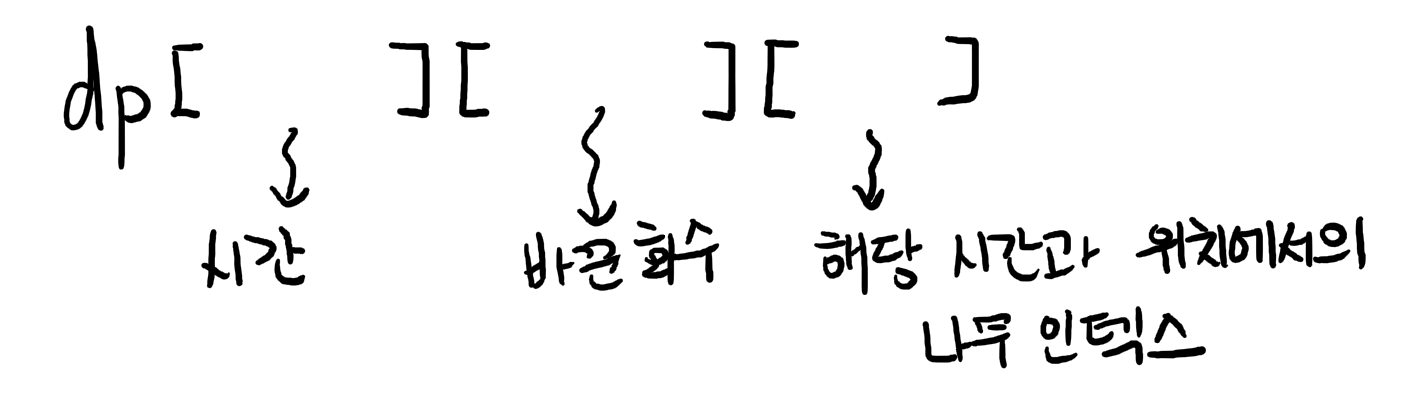
dp 배열은 위와 같이 둡니다.
첫 번째 요소는 시간, 두 번째 요소는 자리를 바꾼 회수, 세 번째 요소는 자두가 떨어지는 인덱스입니다.
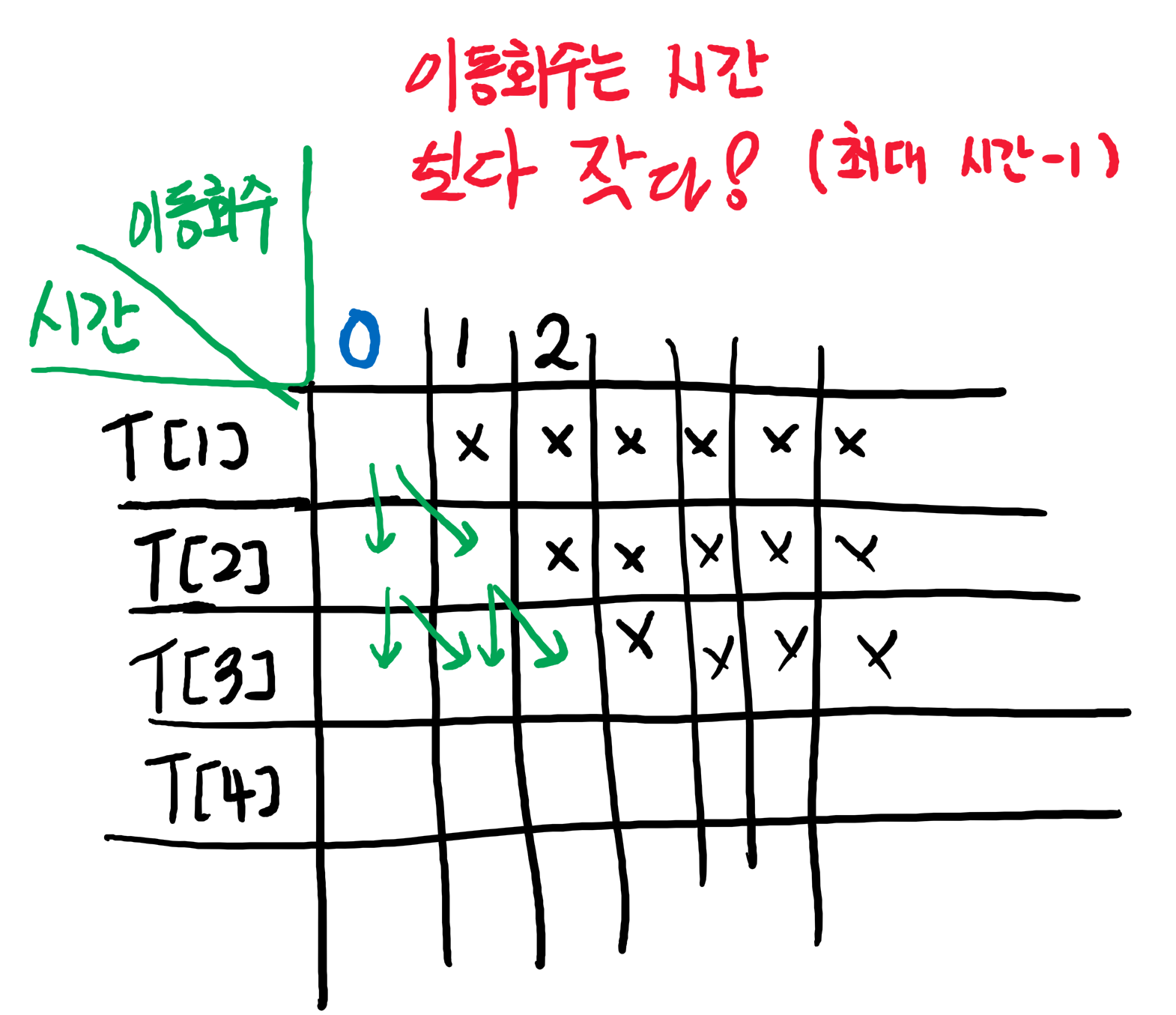
먼저 시간과 이동회수와의 관계를 알아보겠습니다.
시간보다 이동을 더 많이할 수는 없기 때문에 표처럼 절반의 행렬은 x 표시가 되게 됩니다.
만약 현재 시간이 k 라고 하면, k + 1 시간에는 이동회수를 갱신할 때, 이전과 같거나 하나 증가한 이동 회수 만큼 갱신시켜주면 됩니다.
지금시간이 t, 현재 떨어지는 자두가 1이라고 가정합니다.
이전에 이동한 dp[t-1][][]를 기준으로 dp[t][][1] 을 갱신해줘야 합니다.
dp[t][a][1] 는 dp[t-1][a][1] +1 과 dp[t][a][1] 중 큰 값에서 하나를 선택합니다.
dp[t][a+1][1] 는 dp[t-1][a-1][2] + 1과 dp[t][a][1] 중에서 큰 값 중에 하나를 선택합니다.
그리고 이 과정을 하지 않아서 틀렸습니다가 계속 떴습니다.
현재 떨어지는 자두가 1이라고 해도 자신의 위치가 2일 경우가 있습니다.
dp[t][a][2]는 dp[t-1][a][2] 에서의 자두의 값과 같습니다. (자두는 지금 1에서 떨어지기 때문에)
for문을 통하여 먼저 시간을 맞춰주고 바꾼 횟수를 늘려가면서 정답을 구해봅니다.
자세한 구현은 소스코드를 참조하면 됩니다.
데이터가 추가되어 18년 9월 26일부로 소스코드를 수정했습니다.
소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 | #include <iostream> #include <algorithm> #include <vector> using namespace std; #define T_MAX 1000 + 1 #define W_MAX 30 + 1 #define NAMU_POSI 2 + 1 #pragma warning(disable:4996) vector<int> jadoo_time; int T, W; int dp[T_MAX][W_MAX][NAMU_POSI] = { 0 }; int main() { ios::sync_with_stdio(false); cin >> T >> W; jadoo_time.resize(T + 1, 0); for (int t_idx = 1; t_idx <= T; t_idx++) cin >> jadoo_time.at(t_idx); // dp 초기화 if (jadoo_time.at(1) == 2) dp[1][1][jadoo_time.at(1)] = 1; else dp[1][0][jadoo_time.at(1)] = 1; // W는 0번 부터 사용하고 T는 1번부터 사용한다. // 시간을 기준으로 변경한 횟수를 갱신한다. for (int t_idx = 2; t_idx <= T; t_idx++) { for (int w_idx = 0; w_idx <= W && w_idx < t_idx; w_idx++) { // 자두가 시간 t에 1번 나무에 있으면 // 이전 위치가 2번일 때의 값에다가 w_idx+1 인 인덱스 if (jadoo_time.at(t_idx) == 1) { dp[t_idx][w_idx][1] = max({ dp[t_idx][w_idx][1], dp[t_idx - 1][w_idx][1] + 1 }); if (w_idx < W && w_idx < t_idx - 1) dp[t_idx][w_idx + 1][1] = max({ dp[t_idx][w_idx + 1][1], dp[t_idx - 1][w_idx][2] + 1 }); dp[t_idx][w_idx][2] = max({ dp[t_idx][w_idx][2], dp[t_idx - 1][w_idx][2] }); } // 2번에 있으면 else { dp[t_idx][w_idx][2] = max({ dp[t_idx][w_idx][2], dp[t_idx - 1][w_idx][2] + 1 }); if (w_idx < W && w_idx < t_idx - 1) dp[t_idx][w_idx + 1][2] = max({ dp[t_idx][w_idx + 1][2], dp[t_idx - 1][w_idx][1] + 1 }); dp[t_idx][w_idx][1] = max({ dp[t_idx][w_idx][1], dp[t_idx - 1][w_idx][1] }); } } } int answer = 0; // dp에서 시간이 T 일때의 최대값을 탐색하여 출력한다. for (int w_idx = 0; w_idx <= W; w_idx++) answer = max({ dp[T][w_idx][1],dp[T][w_idx][2], answer }); cout << answer; return 0; } | cs |