출처 : https://www.acmicpc.net/problem/1766
문제집 성공
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞은 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 2 초 | 128 MB | 3846 | 1668 | 1257 | 44.417% |
문제
민오는 1번부터 N번까지 총 N개의 문제로 되어 있는 문제집을 풀려고 한다. 문제는 난이도 순서로 출제되어 있다. 즉 1번 문제가 가장 쉬운 문제이고 N번 문제가 가장 어려운 문제가 된다.
어떤 문제부터 풀까 고민하면서 문제를 훑어보던 민오는, 몇몇 문제들 사이에는 '먼저 푸는 것이 좋은 문제'가 있다는 것을 알게 되었다. 예를 들어 1번 문제를 풀고 나면 4번 문제가 쉽게 풀린다거나 하는 식이다. 민오는 다음의 세 가지 조건에 따라 문제를 풀 순서를 정하기로 하였다.
- N개의 문제는 모두 풀어야 한다.
- 먼저 푸는 것이 좋은 문제라면, 반드시 먼저 풀어야 한다.
- 가능하면 쉬운 문제부터 풀어야 한다.
예를 들어서 네 개의 문제가 있다고 하자. 4번 문제는 2번 문제보다 먼저 푸는 것이 좋고, 3번 문제는 1번 문제보다 먼저 푸는 것이 좋다고 하자. 만일 4-3-2-1의 순서로 문제를 풀게 되면 조건 1과 조건 2를 만족한다. 하지만 조건 3을 만족하지 않는다. 4보다 3을 충분히 먼저 풀 수 있기 때문이다. 따라서 조건 3을 만족하는 문제를 풀 순서는 3-1-4-2가 된다.
문제의 개수와 먼저 푸는 것이 좋은 문제에 대한 정보가 주어졌을 때, 주어진 조건을 만족하면서 민오가 풀 문제의 순서를 결정해 주는 프로그램을 작성하시오.
입력
첫째 줄에 문제의 수 N(1≤N≤32,000)과 먼저 푸는 것이 좋은 문제에 대한 정보의 개수 M(1≤M≤100,000)이 주어진다. 둘째 줄부터 M개의 줄에 걸쳐 두 정수의 순서쌍 A,B가 빈칸을 사이에 두고 주어진다. 이는 A번 문제는 B번 문제보다 먼저 푸는 것이 좋다는 의미이다.
항상 문제를 모두 풀 수 있는 경우만 입력으로 주어진다.
출력
첫째 줄에 문제 번호를 나타내는 1 이상 N 이하의 정수들을 민오가 풀어야 하는 순서대로 빈칸을 사이에 두고 출력한다.
예제 입력 1
4 2 4 2 3 1
예제 출력 1
3 1 4 2
풀이
위상정렬의 문제 풀이에는 크게 2가지가 있습니다.
dfs 를 사용하는 풀이와 우선순위 큐를 사용한 문제입니다.
http://jason9319.tistory.com/93
자세한 설명은 위의 링크를 참조하시면 됩니다.
저는 이 문제를 dfs를 이용하여 풀이하려고 했지만 실패했습니다.
이유를 살펴보겠습니다.
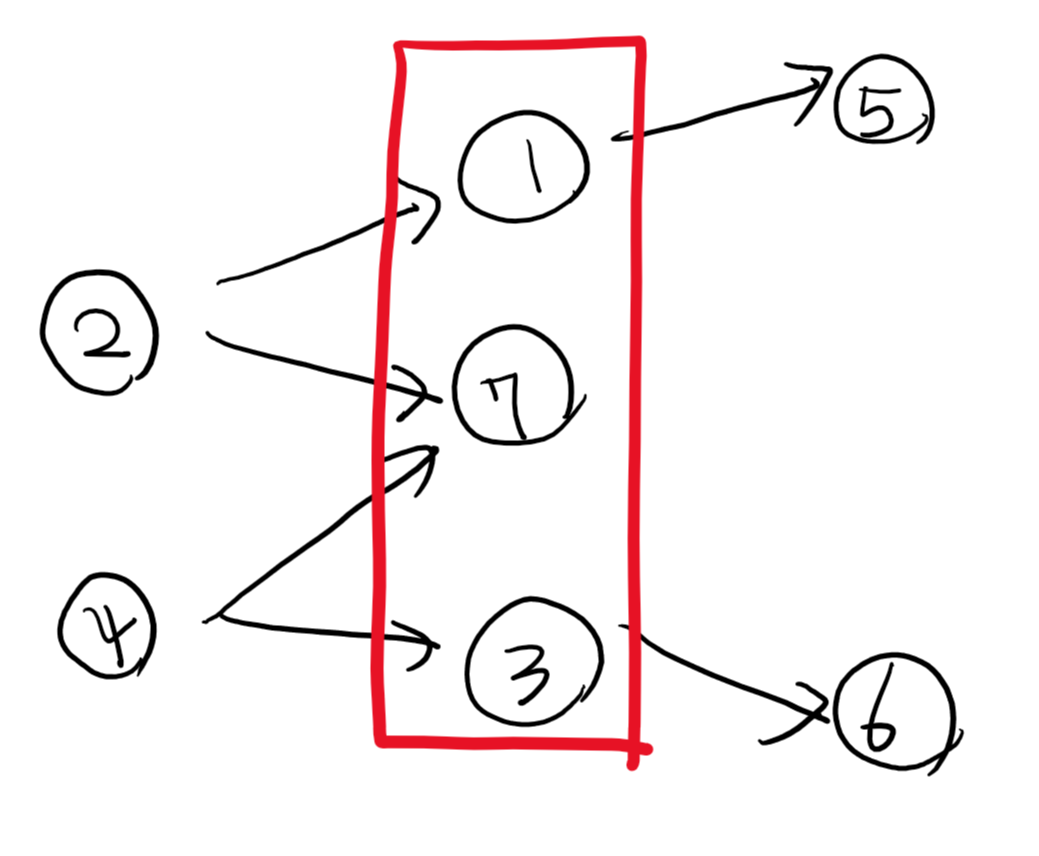
위의 노드 구성을 보자.
먼저 dfs를 4번 노드를 먼저 시작한다.
그러면 스택에 7, 6, 3, 4 순서대로 노드들이 넣어진다.
그리고 2번 노드를 dfs 로 탐색하여 스택에 넣으면 5, 1, 2 순서로 들어간다.
그러면 stack 에서 차례로 빼주면 2, 1, 5, 4, 3, 6, 7 순서대로 나오게 된다.
하지만 이 문제에서 먼저 풀 수 있는 문제는 먼저 푸는 것이 좋다고 하는 조건을 살펴보자.
위의 빨간색 네모로 묶인 문제들은 서로 독립적이기 때문에 문제의 난이도가 쉬운 순서대로 풀어야 한다.
하지만 시작 노드가 여러 개가 있으면(indegree), dfs 와 stack을 이용하면 답이 나오지 않는다.
이 문제는 우선순위 큐를 이용하여 노드들의 indegree를 갱신해주면서 지속해서 탐색하면 된다.
소스코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | #include<cstdio> #include<queue> #include<vector> #include<functional> #pragma warning(disable:4996) using namespace std; const int MXN = 32e3; int main() { int N, M, indegree[MXN + 1] = { 0 }; vector<int> node_vec[MXN + 1]; priority_queue<int, vector<int>, greater<int> > pq; // init scanf("%d%d", &N, &M); for (int m_idx = 0 ; m_idx < M; m_idx++) { int from_, to_; scanf("%d%d", &from_, &to_); node_vec[from_].push_back(to_); indegree[to_]++; } // 0인 indegree 를 먼저 우선순위 큐에 넣는다. for (int i = 1; i <= N; i++) if (!indegree[i]) pq.push(i); // 우선순위 큐를 이용하여 가장 노드의 번호가 앞에 있는 요소를 가져온다. // 현재 가능한 노드들 중에서는 번호가 가장 적은 문제를 먼저 풀어야 되기 때문이다. while (!pq.empty()) { int now_ = pq.top(); pq.pop(); printf("%d ", now_); for (auto next : node_vec[now_]) // 현재의 노드에 연결된 에지의 도착지들의 indegree를 // 감소시켜서 0이면 우선순위 큐에 집어 넣어준다. if (--indegree[next] == 0) pq.push(next); } return 0; } | cs |